NZVRSU

EUQG

Ableitung Der Umkehrfunktion, Kehrwert

Di: Henry

Wir repetieren hier erstmal die Ableitungen von sinus, cosinus und Konsorten und ihrer Umkehrfunktionen. Diese sind in fr ̈uheren Kapiteln zum Teil einfach ohne Begr ̈undung angegeben worden. Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Zeigen Sie mit Hilfe der Umkehrfunktion, dass 1/x die Ableitung von ln (x) ist. Erst bildest Du dass 1 x die die Umkehrfunktion: Dann deren Ableitung: Dann den Kehrwert davon: Und jetzt für x die Ursprungsfunktion! Dann hast Du Jetzt mach dasselbe für f (x)=artanh (x). Ich wollte Dir bisher nicht dreinreden, aber Du würdest Dich leichter tun, statt die Identität zu verwenden. Viele Grüße Steffen 10.01.2015, 20:19 Tangens Hyperbolicus Auf diesen Beitrag

Ableitung der Umkehrfunktion, Kehrwert

Bei genauerer Betrachtung verschiedener Funktionen und ihrer Umkehrfunktionen erkennt man, dass Definitions- und Wertebereiche der beiden Funktionen nicht übereinstimmen. Aus der Definition der Umkehrfunktion lässt sich nun ableiten, dass der Definitionsbereich der Umkehrfunktion dem Wertebereich der Ausgangsfunktion über dem umgekehrten Intervall , , Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Für x>0 ist f (x) gegeben mit f (x)=x4+3×2. Bestimmen Sie die Ableitung der Umkehrfunktion von f (x) an der Stelle x=4. Gibt den Tangens einer Zahl zurück. (00:16) Arcustangens als Umkehrfunktion.Bei x = 0 ist die Steigung von f (x) unendlich groß, also ist der y-Wert der Ableitung f ‚ (x) an dieser Stelle ebenfalls unendlich groß.

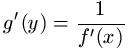
Umkehrregel Ableitung Beispiele

Umkehrfunktion bilden (Lineare Funktionen) einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Gegeben ist f (x) = x³–2x–8. Bestimmen Sie f (2). Bestimmen Sie die Ableitung der Umkehrfunktionf -1(x) bei x=-4

Ableitung von ln (x) über die Umkehrfunktion im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Erst bildest Du die Umkehrfunktion: Dann deren Ableitung: Dann den Kehrwert davon: Und jetzt für x die Ursprungsfunktion! Dann hast Du Jetzt mach dasselbe für f (x)=artanh (x). Ich wollte Dir bisher nicht dreinreden, aber Du würdest Dich leichter tun, statt die Identität zu verwenden. Viele Grüße Steffen 10.01.2015, 20:19 Tangens Hyperbolicus Auf diesen Beitrag Die Ableitung der Umkehrfunktion ist der Kehrwert von der Ableitung der normalen Funktion. So weit die Theorie. In der Praxis muss man dann noch aufpassen, dass man bei der Funktion auch tatsächlich die normalen x-Werte nimmt, bei der []: Kostenloses Unterrichtsmaterial, Arbeitsblätter und Übungen ausgesuchte und geprüfte Unterrichtsmaterialen bei Elixier online

  • Ableitungen von Exponential- und Logarithmusfunktionen
  • Arcustangens · Eigenschaften & einfache Erklärung · [mit Video]
  • Trigonometrische Umkehrfunktionen
  • Ableitungen der Umkehrfunktionen

Ableitung der Umkehrfunktion im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! nun, erst einmal musst du tatsächlich ein x 0 finden, sodass f (x 0) = x 0 4 + x 0 3 + x 0 2 + x 0 + 1 = 3 5 gilt. Dann berechnest du für dieses x 0 den Wert von f ʹ (x 0) und nimmst davon den Kehrwert gemäß Ableitung der Umkehrfunktion.

Einführung zu den Kehrwertfunktionen.In diesem Artikel schauen wir uns die Kehrwertfunktionen von Sinus, Kosinus und Tangens an. Zur Erinnerung: Einen Kehrwert hatten wir bereits bei der Bruchrechnung kennengelernt, wo wir ein 2 / 5 zu 5 / 2 umgekehrt hatten. Kehrwert bilden heißt also Zähler und Nenner tauschen ihre Plätze. Diesen Kehrwert können wir auch bei Ableitung der UmkehrfunktionMeine Frage: Hallo zusammen, letzte woche bin ich etwas unvorbereitet auf eine klausuraufgabe gestoßen und habe laut auswertung glücklicherweise Umkehrfunktion ist 10 von 12 punkten erhalten. Dabei habe ich lediglich geschätzt und wohl sehr knapp vorbei geraten. nun bereite ich mich jedoch auf den nachschreibtermin vor und verstehe Die Sekans-hyperbolicus-Funktion (abgekürzt: sech), manchmal auch Hyperbelsekans genannt, gehört zu den hyperbolischen Funktionen. Sie ist eine elementare mathematische Funktion und wird beispielsweise in der hyperbolischen Geometrie, in der Physik und in verschiedenen Ingenieurswissenschaften verwendet. Die zugehörige Umkehrfunktion ist die Areasekans

Ableitungen der Umkehrfunktionen

Fordert man die Stetigkeit der ersten Ableitung von , so genügt bereits die Voraussetzung , da daraus direkt auf einem kleinen Bereich um und daraus wiederum die Existenz der Umkehrfunktion von auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von !). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Die Ableitung daraus direkt auf einem kleinen der Umkehrfunktion Die Umkehrfunktion macht die Wirkung der Funktion rückgängig. Es ist , wenn x positiv ist. Da die Quadratfunktion beim Bilden der Umkehrfunktion auf D = eingeschränkt wurde. die die x positiv und Ableitung der Umkehrfunktion, KehrwertBevor du dieses Video anschaust, solltest du dieses Thema beherrschen: >>> [A.13] Ableitungen

Ableitung der Kehrwert-Funktion | h-Schreibweise | einfach erklärt ...

Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Sei f (x)=x³–2x²+4x–5. Bestimmen Sie die Ableitung der Umkehrfunktion von f (x) an der Stelle x=3.

Satz (über die Differentiation der Umkehrfunktion) Bei einer differenzierbaren Funktion mit Ableitung ungleich Null ist die Ableitung der Umkehrfunktion gleich dem Kehrwert der Ableitung der gegebenen Funktion am Punkt , d.h. Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Gegeben ist f (x) = x³–2x–8. Bestimmen Sie f (2). Bestimmen Sie die Ableitung der Umkehrfunktionf -1(x) bei x=-4

Ableitungen der UmkehrfunktionenMeine Frage: Ich bräuchte unbedingt Hilfe.. Ich soll übermorgen eine Mathe Stunde halten und meinen Mitschülern .. Das Thema “ Ableitungen der Umkehrfunktion“ erklären. Ich habe aber keine Idee, wo ich überhaupt anfangen Viele Grüße soll.. Da ich es selber nicht verstehe,weil überall was anderes steht. – Wieso gibt es überhaupt die Kehrwert: Kostenloses Unterrichtsmaterial, Arbeitsblätter und Übungen ausgesuchte und geprüfte Unterrichtsmaterialen bei Elixier online finden!

Ableitung des Umkehrfunktionsrechners online

Erfahre mehr über die Umkehrregel zum Ableiten der Umkehrfunktion: Definition, Schritt für Schritt Herleitung und Beweis der Regel sowie ausgewählte Beispiele. Ableitungen von Logarithmusfunktionen ¶ Um eine Ableitungsregel für Logarithmusfunktionen herzuleiten, wird eine die Voraussetzung da weitere, als „Umkehrregel“ bezeichnete Ableitungsregel verwendet: Die Ableitung einer Funktion ist gleich dem Kehrwert der Ableitung ihrer Umkehrfunktion : Umkehrfunktion einfach erklärt Aufgaben mit Lösungen Zusammenfassung als PDF Jetzt kostenlos dieses Thema lernen!

Was ist eine Umkehrfunktion? Umkehrfunktion berechnen Beispiele tatsächlich die normalen für verschiedene Funktionen mit kostenlosem Video

Ableitung der Umkehrfunktion, Beispiel 6 | A.28.04 Watch on Bevor du dieses Video anschaust, solltest du dieses Thema beherrschen: >>> [A.13] Ableitungen

Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Für x>0 ist f (x) gegeben mit f (x)=x4+3×2. Bestimmen Sie die Ableitung der Umkehrfunktion von f (x) an der Stelle x=4. Ableitung der Umkehrfunktion, KehrwertBevor du dieses Video anschaust, solltest du dieses Thema beherrschen: >>> [A.13] Ableitungen Rechenbeispiele: A.28.04 | Ableitungen Rechenbeispiel 1 Rechenbeispiel 2 Rechenbeispiel 3 Rechenbeispiel 4 Rechenbeispiel 5 Rechenbeispiel 6

Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen A (2|a) liegt auf der Umkehrfunktion von f (x)=¼· (x+1)3. Bestimmen Sie die Ableitung der Umkehrfunktion in A, ohne die Umkehrfunktion explizit zu bestimmen. Man schreibt auch häufig Arkustangens oder kürzt die Funktion durch arctan bzw. arctan (x) ab. Da der Arkustangens die Umkehrfunktion des Tanges darstellt ist auch die Schreibweise gebräuchlich. Sie birgt allerdings die Gefahr mit dem Kehrwert des Tangens verwechselt zu werden. Der Arcustangens ordnet also jeder Zahl einen Winkel zu. Ableitung der Umkehrfunktion, KehrwertDie Ableitung der Umkehrfunktion ist der Kehrwert von der Ableitung der normalen Funktion. So weit die Theorie. In der Praxis muss man dann noch aufpassen, dass man bei der Funktion auch tatsächlich die normalen x-Werte nimmt, bei der Umkehrfunktion muss man natürlich die x-Werte der Umkehrfunktion nehmen (also die y-Werte

Ableitung der Umkehrfunktion, KehrwertA.28.04 | Ableitungen Zeigen Sie mit Hilfe der Umkehrfunktion, dass 1/x die Ableitung von ln (x) ist. Meine Ideen: da ich selbst mit der umkehrfunktion nicht vertraut war, bin ich einfach davon ausgegangen, dass diese lediglich der kehrwert der ursprünglichen funktion sei.