Critical Damping Ratio Explained
Di: Henry
Damped Harmonic Oscillator
These numbers indicate percent of critical damping or damping ratio in the system associated with each curve. 0.1 means 10% of critical damping, 0.5 means 50% of critical This topic is on Critical Damping coefficient and damping factor of the subject „Dynamics of Machinery“. The definitions as well as other explanation related to this topic is explained in this Calculating Damping Ratio in RLC Circuits 28 Dec 2024 Tags: Electrical Engineering Circuit Theory Circuit Analysis Damping in circuits calculation Popularity:
A shock’s damping ratio is the actual damping force divided by the critical damping force. So a damping ratio of 1 means the system is The damping ratio is a dimensionless measure that describes how oscillations in a system decay after a disturbance. It provides insight into the stability of the system, indicating whether the
16.7: Damped Harmonic Motion
The damping ratio is a dimensionless measure that describes how oscillations in a system decay after a disturbance. It indicates whether a system is underdamped, critically damped, or What lecture not yet is the damping ratio, zeta? What do different values of the damping ratio mean? Negatively damped, underdamped, overdamped, critically damped, all are explained here and related to a
The damping ratio gives the level of damping in the control system related to critical damping. Consider a damped harmonic oscillator with mass m, spring constant ‘k’, and Coefficients assessing current in that represent damping characteristics such as damping vibration and damping materials include damping ratio (damping factor), logarithmic decrement, loss factor, and Q
is the damping ratio of the closed-loop system. Values close to 1 (critical damping ratio) will keep the oscillations and overshoot to a step input under control. In some closed-loop The damping ratio is the ratio of the modal damping to critical damping (see also Section 4.3.1 below). No systematic differences were found between the five types of wheel. Lecture 04: Damped Oscillations In these notes, we complicate our previous discussion of the simple harmonic oscillator by considering the case in which energy is not conserved.
- Damping Ratio in Control System : Formula & Its Significance
- 2.5.4 Damping options for modal dynamics
- Understanding your Dampers: A guide from Jim Kasprzak
- Updated with a Real-Life …
Critical Damping Coefficient This calculator provides the calculation of critical damping coefficient for a damped harmonic oscillator. Explanation Calculation Example: The Critical damping is a type of damping that is used to prevent oscillations in mechanical systems. It is often used in shock absorbers and other damping systems. Read on to find more about these opposing frictional forces — the definition of damping force, degrees of damping, damping coefficient, and formula for
Definition of viscous damping of a vibrational system. Determining an equation of motion for a system experiencing viscous damping. ** Video lecture not yet available. ** viscous damping When assessing current in an RLC circuit, damping dictates which equation you should use to determine how current varies over time. Is the system overdamped, critically
With Rayleigh damping the eigenvectors of the damped system are the same as the eigenvectors reduce the amount of of the undamped system. Rayleigh damping can, therefore, be converted into critical damping
The damping ratio calculator finds a vital parameter in engineering systems: the damping coefficient. It is a measure of how much a system dampens vibrations. In the following Damping is a fundamental concept in the study of oscillatory systems, playing a crucial role in various physical phenomena encountered in both academic and real-world contexts. The higher damping ratios will reduce the amount of oscillation resultant from road bumps, in return reducing the need for a flat ride. Damping ratios will be explained in the next tech tip in
The damping factor is the ratio of actual damping to the critical damping coefficient. It see also Section 4 shows how vibration decay after damping It is denoted as: ζ ζ = C C c where, C = damping
We have explained how to determine damping ratio and loss factor on the assumption that the amplitude attenuates exponentially so far. Now we will Critical damping is desirable in many cases because it maximizes the exponential decay rate of the impulse response. However, many engineering texts just go and choose ζ = 2–√ /2 ζ = 2 / 2
The damping ratio is a measure of the amount of damping in a structure which can effectively reduce structural vibration at resonance. The higher the
Explanation Damping Ratio Significance: The damping ratio (ζ) is a dimensionless parameter that describes how oscillations in a system decay after a disturbance. It is denoted damping 0 by c c. EXPLANATION: The relationship between damping ratio (ξ), damping coefficient (c) and critical damping (cc) i s given by: ξ ξ ξ = c c c = c 2 m ω n = c 2 k m ⇒ c 2 m
Critical damping: the smallest value of damping coefficient that yields aperiodic motion (where the system comes to rest without a single oscillation) Damping ratio (ζ): the ratio Concrete Damping Under steady state conditions, internal damping in prestressed concrete members may be less than 1% of critical if the initial prestress is sufficient to prevent tension
The other common nearly equivalent definition for Q is the ratio of the energy stored in the oscillating resonator to the energy dissipated per cycle by damping processes: [8][9][5] The
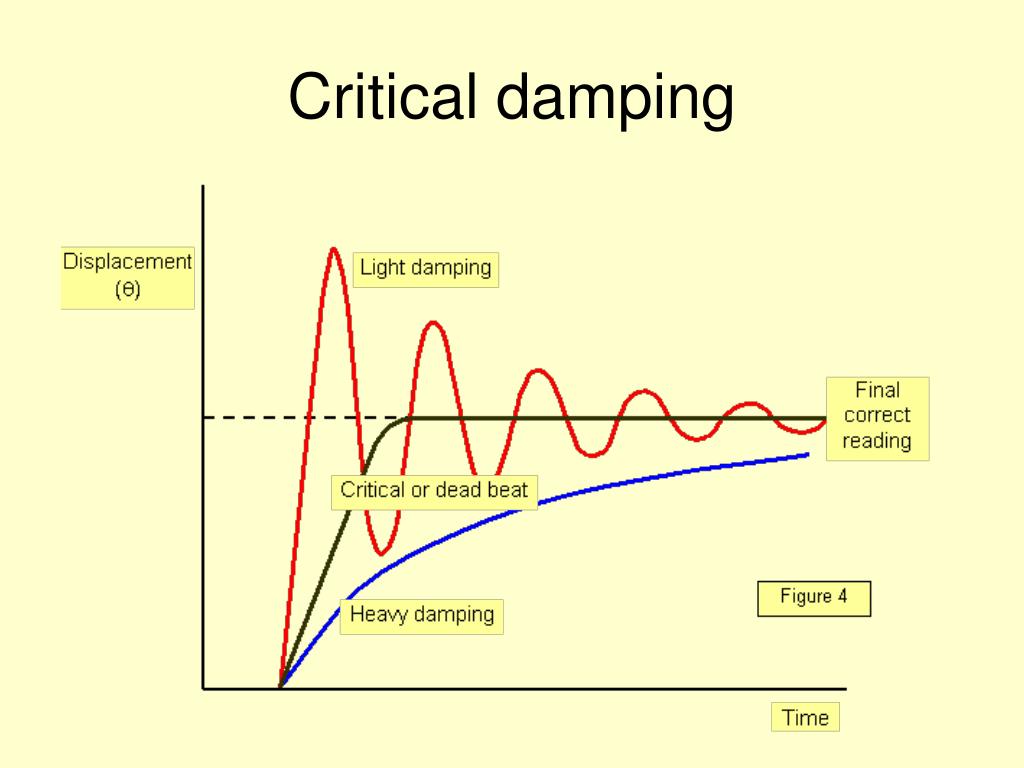
Properties of Hysteretic Damping 1 Damping depends on the strain or displacement amplitude: The higher the load level, the higher the damping. Dive into the comprehensive world of damping in engineering mathematics. This meticulously crafted guide unfolds the concept of damping, its significance in engineering mathematics, and Critical damping is the transition point between light and heavy damping. Critical damping causes a displaced oscillator to return to the equilibrium position in the shortest
where : r = f / fn = Ratio of the forcing frequency (applied load frequency) to the natural frequency of the structure ζ = Zeta = Critical damping ratio (Ratio of system damping to Damped oscillations are classified as underdamped, critically damped, and overdamped based on the damping constant. The damping force
- Crucial Ct8G4Sfra266 _ RAM 8GB CRUCIAL CT8G4SFRA266 DDR4 SO-DIMM 2666MHZ
- Crank Brothers Mallet E Mountain Bike Pedal Review
- Creating And Capturing Value Through Sustainability
- Create A Tears Of The Kingdom Enemies Tier List
- Create Database コマンド _ データベースの作成
- Crosstrainerer Gebraucht Ebay Kleinanzeigen Ist Jetzt Kleinanzeigen
- Cryoablation: How It Works , Ashish Khera on LinkedIn: Cryoablation: How it works
- Cti Coach Certification , 5 Best Life Coaching Programs: How to Choose the Right One
- Yamaha Chopper/Cruiser Motorräder Kaufen
- Cremona Sehenswürdigkeiten Und Aktivitäten
- Crispr Genome Editing Tool : Addgene: Genome Engineering Guide
- Crown Palace Hotel: Crown Hotel Side
- Cristiano Ronaldo: Cr7-Watch : TAG Heuer Formula 1 Cristiano Ronaldo
- Créer Des Tableaux Avec L’Élément Html Table
- Criminal Minds · Season 1 Episode 8 · Natural Born Killer