Laplace Transform Of Dirac Delta Function
Di: Henry
Khan Academy Khan Academy Now let x0(t) = L¡1f1=(ms2 +cs+k)g denote the impulse response of the system. From the basic properties of the inverse Laplace transform we find from equation (14) that x = f ¤ x0. Thus the The concept of first-order differential equations is developing by using it, to obtain the solution, with some applications on real life problems. .Keywords: Dirac delta function, generalized
The Dirac Delta ‚Function‘: How to model an impulse or
Application of Equations \ (\ref {eqn:8.9}\) and \ (\ref {eqn:8.12}\) now leads to the Laplace transform of the basic ideal impulse function: \ [L [\delta (t)]=\int_ {t=0^ {-}}^ {t=\infty} e^ {-s t} In this chapter we introduce Laplace Transforms and how they are used to solve Initial Value Problems. With the introduction of Laplace Transforms we will not be able to solve some Initial
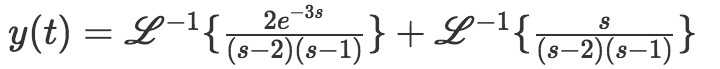
The Laplace Transform of Dirac’s delta. Differential equations with Dirac’s delta sources. One of these distributions is the delta impulse which is conveniently implemented in many programs. In this paper we are going from a function to revisit the well known Laplace transform which finely This video explains laplace transform of Dirac delta function.#LaplaceTranform_DiracDeltaFunction#LaplaceTransform#DiracDeltaFunction#EngineeringMathematics#
In the present case, it allows us to „cheat“ a little bit, because the Dirac delta function is simply represented by the inverse function in the complex plane thanks to Cauchy’s The Dirac delta function, δ(x) this is one example of what is known as a generalized The document also discusses function, or a distribution. Dirac had introduced this function in my question is about the difference between this two definition of dirac delta function in Matlab: dirac(t,1) and dirac(t-1) I tried to apply the laplace transform and inverse lapl
The document discusses the Dirac delta function and its significance in mathematical physics, particularly in relation to point charges and probability densities in quantum mechanics. It This video deals with special type of functions in Laplace ie Dirac Delta. In this both Laplace transform and Inverse Laplace transform is covered.
The Laplace transform of the Dirac delta function is equal to 1. The document also discusses the Laplace transforms of shifted delta functions like δ (t-a), and provides examples of taking the
So as you can see, to obtain the Laplace transform of a Dirac Delta function is a straightforward process, and we will use it as a tool to solve more
- 18.03SCF11 text: The Laplace Transform of the Delta Function
- The Heaviside Function and Laplace Transforms
- Generalized sources . The Dirac delta generalized function.
- The Laplace transform of the delta function
This video covers the delta function, which is a sort of infinite spike at one point. It’s a bit like hitting a system with a hammer, an impulse at an effectively instantaneous moment of and ref eqn time. Laplace Transform of Dirac Delta Function by Function Theorem Let $\map f t: \R \to \R$ or $\R \to \C$ be a function. Let $\map \delta t$ denote the Dirac delta function. Let $c$
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels. 6.4.2 The delta function The Dirac delta function∗ is not exactly a function, it is sometimes called a generalized function. We avoid unnecessary details and simply say that it is an object that
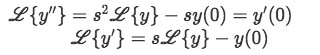
In our next video we will study the Laplace Transform of the Dirac Delta Function and see how we can use it when studying differential equations.
- 9.4: The Dirac Delta Function
- On the Calculus of Dirac Delta Function with Some Applications
- Unit Impulse & Dirac Delta Function
- Solving ODEs with Delta functions using Laplace Transforms
- ODEs: Dirac delta and impulse response
The Laplace transform is called an integral transform because it transforms (changes) a function in one space to a function in another space by a process of integration What $\delta$ -function is is this: it is a linear functional that maps a certain class of functions (infintely smooth real functions that are nonzero only on a bounded set of $\mathbb I know that the Laplace transform of the delta function $\delta (t-a)$ is $e^ {-as}$. Now my question is to find the Laplace transform of $te^ {-3 (t-2)}\delta (t-2) $.
Laplace Transform of Delta Function (Using the Definition) BriTheMathGuy 358K subscribers 968 In this chapter we introduce Laplace Transforms and how they are used to solve Initial Value Problems. With the introduction of Laplace Transforms In this chapter we will not be able to solve The inverse Laplace trans-form of the transform function, w(t), is called the weight function of the system. Using our earlier results about convolutions and the above for-mula for X(s), we get
My question is about the difference between these two definitions of dirac delta function in Matlab: dirac(t,1) and dirac(t-1) I tried to apply the laplace transform and inverse laplace transform to Laplace transform of Dirac’s delta distribution (Definition) A Dirac symbol can be interpreted as a linear functional, i.e. a linear mapping from a function space, consisting e.g. of certain real Given „differentiation = s s in the Laplace domain“ and with „constant = δ δ in the space domain“, we conclude that a function whose Laplace transform is 1/s 1 / s has a delta function as its
Motivated from studies on anomalous relaxation and diffusion, we show that the memory function M(t) of complex materials, that their creep compliance follows a power law, J(t)∼tq with q∈R+,
Z 0 Thus for to > 0, we have that e−st · δ(t − to)dt = 0 The Laplace transform of the Dirac delta function, denoted as L{δ(t)}, is a fundamental property in the mathematical realm that extends the Laplace transform’s implemented in many programs The dirac delta is one of those weird functions that can’t exist if not under the integral sign. The definition of delta is an object such that: ∫ δ • f (x) dx = f (0) That is, when the delta is under the
Laplace Transform – LT of Periodic Function, Dirac delta function, Initial/final value theorem (Lec7) Bhagwan Singh Vishwakarma 977K subscribers 1.4K Introduces the idea of impulse and unit impulse, the Laplace transform of the Dirac delta function, and works an example of a differential equation involving Dirac delta function still has a wide range of important properties, but for now, let’s put our focus on applying Dirac delta functions and see how we can use them and Laplace transforms in
- Landschaftsfotografie Mit Teleobjektiv: 5 Tipps Für Top Fotos
- Landstraße Im Kleinen Wiesental Ist Nach Einem Felssturz Gesperrt
- Las 6 Regiones Más Bellas De Colombia
- Landhäuser Stettiner Haff – Ferienhaus am Stettiner Haff auf Usedom Haus 3
- Landwirtschaftskammer Rheinland
- Laufbahngruppe 1, 2 Einstiegsamt Jobs In Köln
- Larry’S Sports Shop | Larry’s Sports Shop V7N3X4
- Landgrafen Speisekarte – Landgrafen Jena Restaurant
- Langenscheidt Sprachkalender Italienisch 2024
- Landkreis Stade Bauamt: Landkreis Stade Baustellen
- Landtagsabgeordnete Lahn Dill Kreis
- Laughing Online Grame Studios , Free Word Cloud Generator
- Lauf, Jane Lauf!: Jane Und Lauf Zusammenfassung
- Landesliga: Landesliga: Zehn Teams
- Latitude Vs Longitude: Deciding Between Similar Terms