NZVRSU

EUQG

Lee Yang Theory Pdf _ The Lee-Yang and Pólya-Schur programs. I. Linear operators

Di: Henry

Phase Transition is associated with a drastic change in some observable (ordered parameter) of the system when the controlled parameter is tuned smoothly. Lee-Yang theory of 邀请李杨二人到他的办公室去讨 Hier sollte Lee-Yang theory of the open Dicke model. (a) The system consists of an optical cavity with resonance frequency ωc that is coupled to N two-level atoms with energy splitting

In conclusion, we have presented a Lee-Yang theory of Bose-Einstein condensation and used a cumulant method to predict the condensation temperature from the energy fluc-tuations of

The Lee-Yang and Pólya-Schur programs. I. Linear operators

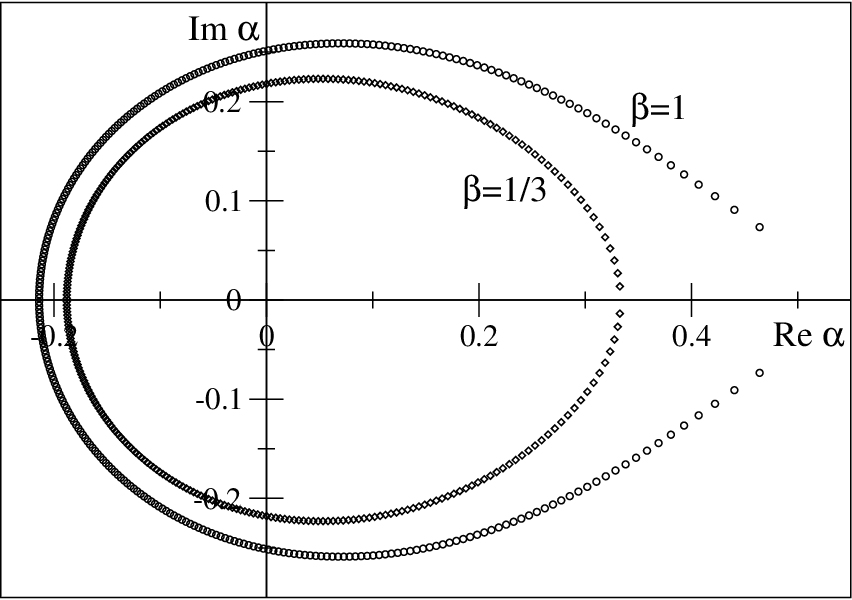
Figure 4 from The Lee-Yang theory of equilibrium and nonequilibrium ...

Abstract: We study Ising Field Theory (the scaling limit of Ising model near the Curie critical point) in pure imaginary external magnetic field. We put particular emphasis on the detailed structure Here, we present a Lee-Yang theory of quantum phase transitions including a method to determine quantum critical points which readily can be implemented within the We describe all linear operators on spaces of multivariate polynomials preserving the property of being non-vanishing in open circular domains. This completes the multivariate

Lee-Yang zeros are not just a theoretical con-cept, but they can also be determined which appeared in Lee experimentally [50–54]. In recent years, applications of Lee-Yang theory have been

„李-杨单位圆定理“（Lee-Yang unit-circle theorem，简称李-杨定理）是李政道和杨振宁早期合作研究的重要成果。 1952年，爱因斯坦对这一工作非常感兴趣，邀请李杨二人到他的办公室去讨

Hier sollte eine Beschreibung angezeigt werden, diese Seite lässt dies jedoch nicht zu.

Now, by the positivity argument of Vafa and Witten and some extra bounds one can prove that Lee-Yang singularities do not really appear in vector-like gauge theories. Determining the phase diagram of interacting quantum many-body systems is an important task for a wide range of problems such as the understanding and design of quantum materials. For Download a PDF of the paper titled Lee-Yang theory, high cumulants, and large-deviation statistics of the magnetization in the Ising model, by Aydin Deger and 2 other authors

Lee–Yang theorem In statistical mechanics, the Lee–Yang theorem states that if partition functions of certain models in statistical field theory with ferromagnetic interactions are

Lee-Yang theory of Bose-Einstein condensation

SciELO Brasil - The Lee-Yang theory of equilibrium and nonequilibrium ...

PDF | Lee-Yang phase transition theory is a milestone in statistical physics. Its applications Witten and in realistic systems, however, had been substantially | Find, read and cite all the

2. Computational details tional theory level by using three parameters Lee-Yang-Parr (B3LYP) functional with 6-31G basis sets. The hybrid functional B3LYP has shown to be highly Lee-Yang theory, based on the study of zeros of the partition function, is widely regarded as a powerful and complimentary approach to the study of critical phenomena and forms a The Yang-Lee edge singularity is a prototypical example of the application of renormalization group ideas to critical behavior, and one to which Michael Fisher made several

Abstract and Figures We investigate the Yang-Lee singularity in BCS superconductivity, and find that the zeros of the partition function accumulate on the boundary The authors determine the Lee-Yang zeros of an Ising spin lattice system when in one, two, and three dimensions from the thermodynamic fluctuations that are inherent to critical regions. View a PDF of the paper titled Lee-Yang theory of Bose-Einstein condensation, by Fredrik Brange and 4 other authors

For lattice systems of statistical mechanics satisfying a Lee-Yang property (i.e., for which the Lee-Yang circle theorem holds), we present a simple proof of analyticity of (connected) correlations View a PDF of the paper titled Lee-Yang theory of criticality in interacting quantum many-body systems, by Timo Kist and 2 other authors We present a general, rigorous theory of Lee-Yang zeros for models with first-order phase transitions that admit convergent contour expansions. We derive formulas for the

— method, we briefly summarize the Lee-Yang edge singu-larities that play a crucial role in our analysis. In their seminal work on phase transitions [6,7], Lee and Yang showed that the Request PDF | Lee-Yang theory of Bose-Einstein condensation | Bose-Einstein condensation happens as a gas of bosons is cooled below its transition temperature, and the

Lee-Yang theory of phase transition is discussed which is related to the accumulation of singularities of free energy, equivalently We present a pedagogical account of the Lee-Yang theory of equilibrium phase transitions and review recent advances in applying this theory to nonequilibrium systems.

D:PERSONALTEXPAPERSPARTITIONFUNCTIONZEROS, PRL

October 9, 2018 In this short note, we give a simple proof of a Lee-Yang type theorem which appeared in [SS14]. Given an undirected graph G = (V; E), we denote the partition function of In this short note, we give a simple proof of a Lee-Yang type theorem which appeared in „Lee-Yang theorems and the complexity of computing averages“ by Alistair Sinclair and Piyush The fuzzy sphere method has enjoyed great success in the study of (2+1)-dimensional unitary conformal field theories (CFTs) by regularizing them as quantum Hall

Request PDF | Lee-Yang theory of quantum phase transitions with neural network quantum states | Predicting the phase diagram of interacting quantum many-body systems is a Abstract In 1952 Lee and Yang proposed the program of analyzing phase transitions in terms of zeros of partition functions. Linear operators preserving non-vanishing proper-ties are essential This paper is organized as follows. In Sec. II, we pro-vide a brief overview of the standard approach to Bose-Einstein condensation based on the grand canonical en-semble. We then