NZVRSU

EUQG

Minterms Row 0 – Minterms and Maxterms Calculator

Di: Henry

The canonical SOP form represents the function as a sum of minterms (product terms where each variable appears once, either complemented or uncomplemented). From the truth table, we identify rows where Y = 1: Learn how to solve a 4-variable K-Map with this step-by-step guide. Obtain the truth Understand the process of grouping minterms and simplifying Boolean expressions. Notice how the operation (AND for minterms, OR for maxterms) and the criteria for negation (when the input variable is 1 for minterms and when it is 0 for maxterms) are opposite of each other.

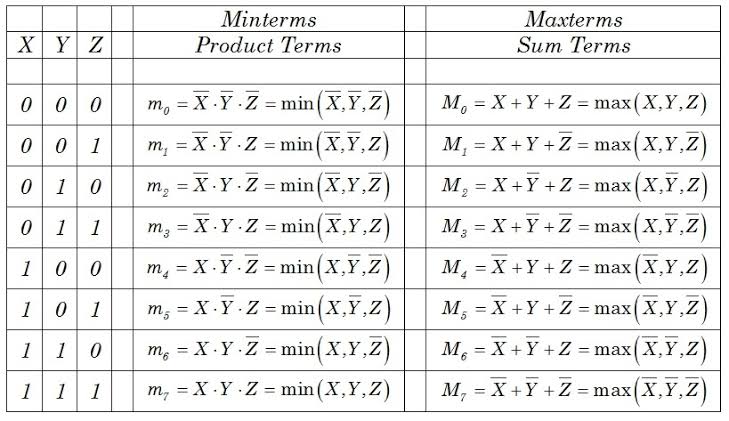
How to solve minterm and maxterm through K-map - Franklyexplained

Canonical functions Table of contents Introduction Truth table formation Truth table formation Sum of product expressions (SOP) Product of sum expressions (POS) Canonical expressions Minterms Maxterms Conversion of canonical forms Conversion from minimal to canonical forms Minimal POS to canonical POS Minimal SOP to canonical SOP Example algebraic To write the maxterm consider the rows which has the output F=0. In the above truth table M0, M2, M4, M6 have outputs ‘0’. The input which has the value the aim is to minimize ‘0’ is written as such and the input which has the value ‘1’ is complimented. For example in the row 2, the output F=0 and the inputs A=C=0 and B=1. Concepts Karnaugh Map (K-map), Boolean Algebra, Minterms, Minimization, Grouping of 1s, SOP (Sum of Products) Form Explanation Given a Boolean function expressed as the sum of minterms Σm(1,11,12,13,15), the aim is to minimize it using a Karnaugh Map. Each minterm corresponds to a binary value of the input variables where the function outputs 1. We

Minterms and Maxterms Calculator

If we partition an event F into component events whose probabilities can be determined, then the additivity property implies the probability of F is the sum of these component probabilities.

If both the minterms in the column are not circled, then apply logic 0 to the corresponding data input. Hence apply 0 to D_5. If only the minterm in the second row is encircled then C should be applied to the data input. If only the minterm in the first row is encircled, then C ̅ should be connected to the data input.

The document discusses gate-level minimization and optimization methods for digital circuits. It describes the Karnaugh map method, which provides a pictorial representation of a truth table using a grid of squares. Each square represents a minterm. Adjacent minterms can be combined to simplify Boolean functions. Several examples demonstrate using K-maps to minimize

– Row 2: A’B’C – Row 5: AB’C‘ – Row 6: AB’C – Row 7: ABC‘ – Row 8: ABC ***Step 4: Sum of Minterms*** Combine these minterms to express F as a sum of minterms. F = A’B’C + AB’C‘ + AB’C + ABC‘ + ABC #### Final Answer F = Σ (m1, m4, m5, m6, m7) #### Summary The Boolean function F = A + B’C was expressed as a sum of minterms by constructing a This chapter covers minterms and maxterms, use of K-map to simplify Boolean function, Boolean function representation in the form of sum of product (SOP) and product of sums (POS), and application of universal gates (NAND and OR).

Solution For A smart alarm system activates (output = 1) when: Motion is detected and the door is open (OR) the window is open and no one is at home.

  • Solved Part A A logic circuit has inputs A, B, C,
  • Minterms and Maxterms Calculator
  • Minterms, Maxterms, Karnaugh Map , and Universal Gates
  • MINTERM TO TRUTH TABLE CONVERTER

Find local businesses, view maps and get driving directions in Google Maps. Boolean Function Definition and Minterm Representation The question asks us to simplify a given Boolean function F F using three digital input signals: A, B, and C. A is specified as the Most Significant Bit (MSB), and C as the Least Significant Bit (LSB). The Boolean function is defined as a sum of specific minterms: F = m 0 + m 2 + m 3 + m 5 + m 7 F = m0 + m2 + m3 + m5 + m7 F Combinational Circuit with Four Inputs and One Output A combinational circuit has four inputs and one output. The output is equal to 1 when: All the inputs are equal to 1, or None of the inputs are equal to 1, or An odd number of inputs are equal to 1. Tasks: (a) Obtain the truth table. (b) Find the simplified output function in sum of products. (c) Find the simplified output function in

Switching Algebra and Logic Circuits - ppt download

Learn Quine-McCluskey tabular method for Boolean expression minimization. Includes prime implicants, cover tables, and examples. Digital logic design.

Ideas for Solving the Problem Truth Table Construction: Create a truth table for the given Boolean function to determine the output (f) for all possible combinations of inputs (a, b, c). Min Term 每个乘积项是minterm 用二进制数表示 而每个和项是maxterm 同样以二进制数呈现 Identification: Identify the rows in the truth table where the output f is 1. These rows correspond to the min terms of the function. Sum of Min Terms Expression: Express the function as a sum of

WHAT IS TRUTH TABLE TO MINTERM CONVERTER? Truth table to minterm converter, Finds the sum of minterms representation of the constructed truth table, Gives the result in both 0 D 1 brief and explicit forms. HOW TO USE THE TRUTH TABLE TO MINTERM CONVERTER? You can use the truth table to minterm converter in two ways. USER INPUTS You can click on any row

The order of the minterms would be (in the top row), 0,2,6,4 and (in the bottom row) 1, 3, 7, 5. This evaluates to 1 since the ‚don’t cares‘ can be whatever value (1 or 0). And in this case the numbering scheme is 0, 1, 3, 2 in the first row 4, 5, 7, 6 in the second row 12, 13, 15, 14 in the third row and 8, 9, 11, 10 in the fourth row.

(0,4) (4,5) (5,13) (13,15) (11,15) 0 X 4 XX 5 XX 11 X 13 XX 15 XX We cross out columnsA0C0D0andACDand mark them with asterisks, to indicate that these are essential. Each row intersected by one of these columns is also crossed out, because that minterm is now covered. At this point, prime implicantBC0Dcovers 2 remaining ON-set minterms (5 and 13). Determine the minterms (rows where the function is 1) and maxterms (rows where the function is 0) from the truth table. A minterm is a specific type of product term in Boolean algebra that represents a unique combination of variables, where each variable can be either true (1) or false (0). Each minterm corresponds to exactly one row in a truth table where the output is true, making them essential for expressing and simplifying Boolean functions. Minterms are often used in the construction of

Solution For Question: Simplify the function F (A, B, C, D) = \sum m (0,2,5,6,7,13,14,15) + d (8,10) using Karnaugh Map (K-map) and implement the simplified function Plot the function: Identify the minterms (for SOP) or maxterms (for POS) from the Boolean function or truth table and place them in the K-map. Group adjacent cells: Group the 1s (for SOP) or 0s (for POS) in rectangles of size 1, 2, 4, or 8. Groups must contain powers of 2, and the larger the group, the simpler the expression.

1. How do I know that expression holds for every single row in the truth table? Sum of Products form is used when you are creating a Disjunctive Normal Form. Each row represents a minterm or a product of literals and the expression is the sum of products (ie. minterms). The sum or disjunction is a logical-OR. So, we don’t care about of each the rows where it is Lecture 4 Minterm and Maxterm Conversion of English sentences to Boolean equations. In the truth table of a Boolean function, each row that yields the output 1 corresponds to a minterm. Minterms collectively represent the function by summing (ORing) all such products. In contrast, each row that yields 0

The implementation table has all the inputs (D 0, D 1, D 2, D 3,) for the multiplexer, under which, all the minterms are listed in two rows. The first row consists of all minters where A is complemented and the second row has First row lists all those minterms where “input variable” is complemented (say 0). Second row lists all those minterms where “input variable” is in its normal form (say 1).

布尔代数中的最小项（Minterm）和最大项（Maxterm）是规范SOP和POS形式的基础。每个乘积项是minterm，用二进制数表示，而每个和项是maxterm，同样以二进制数呈现。对于n变量逻辑函数，有2^n个最小项和最大项。真值表中，输出为1对应minterm，输出为0对 The essential prime implicants are obtained by combining minterms m = 0,3,8,10 to get the term B’D‘ and m = 5,7,13,15 to get the term BD This for POS in rectangles of leaves the minterms m = 9, 11, 3 which may be covered using prime implicants in multiple Boolean Algebra expression simplifier & solver. Detailed steps, Logic circuits, KMap, Truth table, & Quizes. All in one boolean expression calculator. Online tool. Learn boolean algebra.

Why do we need minterms in the first place? We do not need minterms, we need a way to solve a logic design problem, i.e. given a truth table, find a logic circuit able to reproduce this truth table. Obviously, this requires a methodology. Minterm and sum-of-products is mean to realize that. Maxterms and product-of-sums is another one. In either case, you get an algebraic Hmmm, but from your first diagram, you made 3 groups of four ones which basically correspond to A‘ + B + C‘. As such doesn’t this grouping make that expression a valid sum of minterms?

through m15 is obtained. T o accommodate these 16 minterms, 16 cell K- Map is used. Minterms m0 to m2 are placed in Row 0. Note the position of m2 and m3. Minterm m2 is placed in cell 3, whereas m3 is placed in cell 2. In row1, minterms m4, m5, m6 and m7 is placed. Tool for calculating Minterms (canonical disjunctive normal form) and Maxterms (canonical conjunctive normal form) from a truth table of a unknown Boolean expression. b) Simplification using Karnaugh Map Let’s construct the K-map for F 1(A,B,C). List all minterms: ABC ′: A =1,B = 1,C = 0 → minterm 6 AB′C: A =1,B = 0,C = 1 → minterm 5 AB′C ′: A= 1,B = 0,C = 0 → minterm 4 A′BC: A = 0,B = 1,C = 1 → minterm 3 A′BC ′: A= 0,B = 1,C = 0 → minterm 2 A′B′C: A= 0,B = 0,C = 1 → minterm 1 Marking these on a 3-variable K-map (A: rows, BC