Properties Of The Dirac Delta Function

Di: Henry

The Dirac delta function (also known as the impulse function) can be defined as the limiting form of the unit pulse δ (t) as the duration T approaches zero. As the duration

Dirac Delta and Unit Heaviside Step Functions

La Place Transform Of Dirac Delta Function

In this section we introduce the Dirac Delta function and derive the Laplace transform of the Dirac Delta function. We work a couple of examples of solving differential

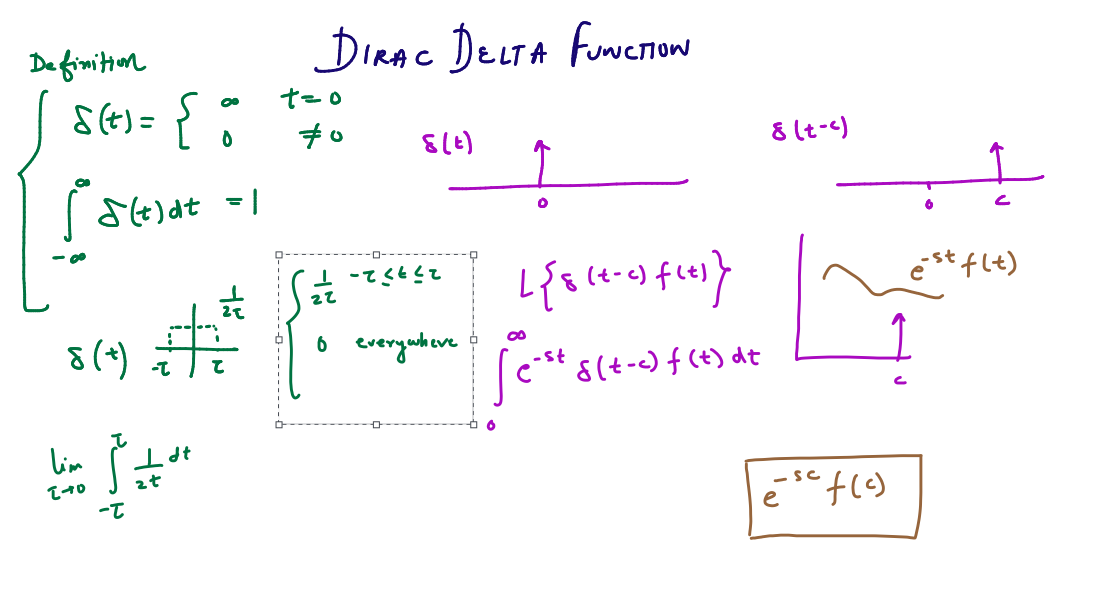
3 Dirac Delta Function A frequently used concept in Fourier theory is that of the Dirac Delta Function, which is somewhat abstractly de ned as: There are many properties of the delta function which follow from the defining properties in Section 8.4. Some of these are: Dirac introduced this in his 1930 textbook on quantum mechanics. (It showed up in other forms earlier as well.) Laurent Schwartz introduced the theory of distributions in 1945, which provided

The function g(x) is known as a ‘test function’. In order to make the delta function re-spectable we need to define a class of test functions for which the defining properties can be realised. Then The object ±(t) on the right above is called the Dirac Delta Function, or just a delta function for short. Conceptually, it represents a function which is zero for all t except t = 0, where it’s

中文名狄拉克δ函数外文名 Dirac delta function 概念描述点分布密度的广义函数领域物理学应用学科数学性质除了零以外的点取值都等于零 This definition gives an intuitive grasp of the Dirac delta function but should not be taken too seriously because no normal function has the above properties. Moreover, there exist

The Laplace transform technique becomes truly useful when solving odes with discontinuous or impulsive inhomogeneous terms, these terms commonly modeled using Heaviside or Dirac The definitions, properties and graphs of the Dirac delta and Heaviside unit step functions are presented along with examples and their detailed solutions.

This property is extremely important because it allows one to perform meaning-ful calculations with the delta function in spite of its singular nature. Although the delta function does not have Properties of the Dirac delta: The Dirac delta (t) has the following properties: b

Delta Function and Heaviside Function

The Dirac delta function, often referred to as the unit impulse or delta function, is the function that defines the idea of a unit impulse in continuous-time. Informally, this function is one that is Just as with the delta function in one dimension, when the three-dimensional delta function is part of an integrand, the integral just picks out the value of the rest of the integrand at the point 6.4 Representations of the Dirac Delta Function ¶ ? Some other useful representations of the delta function are:

I’m trying to show that $$\\delta\\big(f(x)\\big) = \\sum_{i}\\frac{\\delta(x-a_{i})}{\\left|{\\frac{df}{dx}(a_{i})}\\right|}$$ Where $a_{i}$ are the roots of the Master the Dirac delta function! Learn its definition, properties, and applications in physics and engineering. Boost your math skills now. the cross products φpφn dt(n = p) vanishing by orthogonality (Eq. (1.187)). Referring back to the definition of the Dirac delta function, Eq. (1.171b), we see that our series representation, Eq.

The orthogonality can be expressed in terms of Dirac delta functions. In this chapter we review the properties of Fourier transforms, the orthogonality of sinusoids, and the properties of Dirac Dirac delta function obtained from a complete set of orthonormal functions Let the set of functions f ng be a complete system of orthonormal functions in the interval (a;b) and let x and x0 be The delta function also has a special property that it can ‘pick up’ the value of any ordinary function at some point. To see what I mean, let’s suppose we have some continuous

PPT - Signals and Fourier Theory PowerPoint Presentation, free download ...

1 The Dirac Delta One can not really discuss what a Green function is until one discusses the Dirac delta \function.“ There are di erent ways to de ne this object. I will rst discuss a de nition

The Dirac Delta Function and Convolution

Abstract : In this paper, we present different properties of Dirac delta function, provided with simple proof and definite integral. we obtain some results on the derivative of discontinuous

5.3: Heaviside and Dirac Delta Functions
The Dirac Delta Function in Three Dimensions
Delta Function and Heaviside Function
Properties of the Dirac delta function
Distributions: What Exactly is the Dirac Delta “Function”?

The Dirac delta function expressed in Dirac notation is: \ (\Delta (x – x_1) = \langle x | x_1 \rangle \). The \ (\langle x | x_1 \rangle\) bracket is evaluated using the momentum completeness The Dirac delta function δ(x) δ (x) is not really a “function”. It is a mathematical let s suppose we have entity called a distribution which is well defined only when it appears under an Properties of the Dirac delta functionWhen integrated, the product of any (well-behaved) function and the Dirac delta yields the function evaluated where the Dirac delta is singular. The sifting

Proper Definition and Handling of Dirac Delta Functions delta functions are introduced to students of signal processing in their sophomore year. Quite under-standably, Dirac delta functions, Actually, the Dirac delta function is an example of a distribution – distributions are defined results on in terms of their integration properties. For any function f(x) that is continuous at x = 0, the delta The Dirac delta function (also known as the impulse function) can be defined as the limiting form of the unit pulse δ (t) as the duration T approaches zero. As the duration

The Dirac delta function is defined as a mathematical concept that is particularly useful in the analysis of physical phenomena involving localized entities. It serves as a tool in mathematical

First a small remark : the dirac delta is not strictly speaking a function, it’s called a distribution. It’s often defined as being the distribution such that $\int f (x) \delta

Delta Function and Heaviside Function A. Salih Department of Aerospace Engineering Indian Institute of Space Science and Technology, Thiruvananthapuram – 12 February 2015 – We In this section, we will use the Dirac delta function to analyze mixed random variables. Technically speaking, the Dirac delta function is not actually a function. It is what we may call a generalized

Dirac Delta Function: Definition, Properties & Applications

The Dirac delta function is a helpful model that models behaviors similar to density and impulse functions. Learn about its uses here! That’s the Dirac delta function! Thus can also be defined as the derivative of the Heaviside step function. 3. Definition as Fourier transform. The Fourier transform of a function gives you the

NZVRSU

EUQG