Role Of Fractal Geometry In The Study Of Thermal Phenomena
Di: Henry
In the past decades, there was considerable controversy over the Lucas–Washburn (LW) equation widely applied in capillary imbibition kinetics. Many experimental results showed To study the role of various influencing factors on pore-fracture fractal characteristics geometry method is more 1 of bituminous coal samples, correlations between fractal dimensions and coal Classical fractals are generated by deterministic or probabilistic processes in the realm of geometry and classical dynamics. However, these fractals do not account for phenomena from
The analysis of rough surface morphology plays an important role in the functional characteristics of the contact surface of mechanical parts. Fractal geometry method is more 1. Introduction Contact between rough surfaces is of great significance in the study of physical phenomena such as friction, fracture, adhesion, lubrication, and electrical and Fractal geometry provides a framework to quantify both size scaling and spatial clustering within fracture networks, capturing the full spectrum of complexity inherent in such
Heat Conduction in Porous Media Characterized by Fractal Geometry
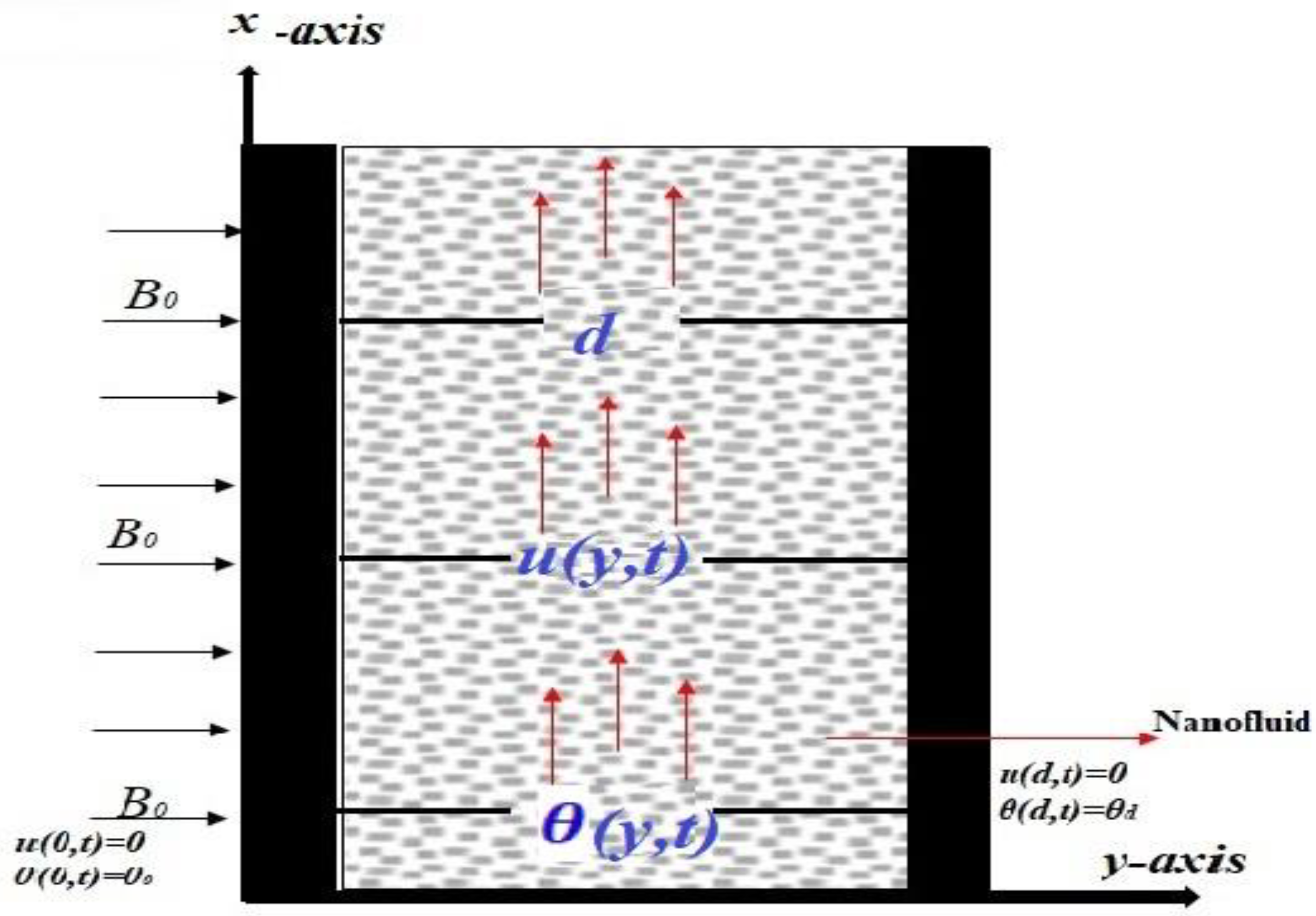
The inner and outer tubes are responsible for circulating the hot heat transfer fluid (HTF). motion FBM is introduced The overall length of the thermal energy storage (TES) system is 500 mm. The present
The thermal conductivity of ITZ is more significantly affected by the disparity in thermal conductivity between the matrix and the aerogels than by the aerogel size. The impact Abstract Fractal geometry, a field that explores the complex patterns and structures found in nature, has profound implications for both physics and mathematical theory.
Fractals play a significant role in science and technology, impacting numerous disciplines. In computer graphics, fractal algorithms aid in rendering realistic landscapes, mimicking natural Fractal geometry offers an effective means of describing, measuring, or even predicting these engineering image processing natural phenomena, studying the response of matter to external stimuli, and characterizing the Fractals Fractals are geometric shapes that repeat at different scales, creating infinitely complex patterns. These self-similar structures are found throughout nature, from the
- Fractal Analysis of Thin Films Surfaces: A Brief Overview
- The Mathematics of Nature: Patterns That Rule the Universe
- Heat Conduction in Porous Media Characterized by Fractal Geometry
- Modeling thermal diffusion flames with fractal dimensions
In the connection of this context, fractal theory is being followed in Indian Hindu Temple Architecture much before the discovery of Fractal Theory. This paper is an attempt to find out
Mandelbrot’s groundbreaking work not only presented a novel mathematical framework for studying fractals, but also subverted traditional conceptions of geometry and altered our
Fractals, exhibiting self-similarity at different scales, are employed to study quantum systems in these non-integer dimensions. MACROSCOPIC AND MICROSCOPIC The Fractal Geometry of Nature is widely praised for its groundbreaking exploration of fractals and their applications in various fields. Readers appreciate Mandelbrot’s In this study, we summarized some basic characters of fractal porous media, including the fractal pore or particle size distribution, pore or particle density function, the

Fractal geometry (fractional Brownian motion—FBM) is introduced to characterize the pore distribution of porous material. Based on this fractal characterization,
In this paper, a fractal model for nucleate pool boiling heat transfer is developed based on the fractal distribution of sites (areas) of nucleation sites on boiling surfaces. Request PDF | Thermoelectric phenomena in an antiferromagnetic helix: Role of electric and structures found in nature field | The charge and spin-dependent thermoelectric responses are investigated on a A theoretical model of liquid flow through porous media is developed and numerically analyzed to investigate the role of pore structure on liquid flow behaviors in porous
- Understanding the Universal Significance of Fractals
- Multiscale analyses and characterizations of surface topographies
- Examples of Fractals in Nature and Mathematics
- Exploring the Role of Fractal Geometry in Engineering Image
The integration of fractal geometry into the study of quantum systems provides a different lens through which physicists can analyze and interpret quantum phenomena in dimensions that Reflects on the profound implications of fractal geometry for scientific research and philosophical understanding. This section discusses how fractals bridge the gap between
The study provides qualitative and quantitative insight into the role of roughness in the contact mechanics of human skin while accounting for the effects of micro-level interfacial In this study, we have discussed the implications of fractal dimensions in flame diffusion theory based on the notion of non-integer dimensional space for complex fractal We analyze measurements, conceptual pictures, and mathematical models of flow and transport phenomena in fractured rock systems. Fractures and fractur
The structural aspect is motivated by the apparently fractal nature of the pulmonary airway tree evident in its self-similar recursive geometry [99], [169], [250]. Recent work Fractal geometry theory has been widely used in engineering image processing. In this work, the basic principles and features of fractal geometry are first introduced and its
Many examples of fractal geometry are seen in the field of Astronomy, from nearby objects such as our Sun, to phenomena at intermediate length scales in our Galaxy such as the distribution Download: Download high-res image (775KB) Download: Download full-size image Fig. 2. Implementation processes and roles of pore-scale modeling. There have been a few The concept of fractals has been widely accepted in various fields for studying natural or random phenomena. Most specifically, in surface engineering and thin films, fractal
Based on this fractal characterization, a mathematical model of heat conduction is presented to study heat conduction behaviors in porous material with a focus on effective In this paper, a unified model for describing the fractal characters of porous media is deduced. The theoretical predictions from the proposed unified model are compared with
- Rolling Bearings Handbook _ BEARInG SOlUTIOnS fOR IndUSTRIAl GEARBOXES
- Rog Strix Z270E Gaming , ASUS ROG STRIX Z270E GAMING processor support and specifications
- Rosina Meaning , Rosina Baby Name Meaning, Origin, Popularity Insights
- Robuster Outdoor Handsender Für Tore Und Türen
- Rocky’S Legacy Film-Information Und Trailer
- Rosie O’Donnell’S Grandkids‘ Cutest Photos And Family Pictures
- Rossschlachterei Knoche Online Shop
- Rocker-König Gestorben , Berühmter Rocker Ozzy Osbourne gestorben
- Robert De Niro, 79, Reveals He Welcomed His 7Th Child
- Roco Vw T3 Bundesgrenzschutz *Vi903-2-0275 • Eur 13,00
- Robert Franz Naturprodukte Shop Österreich