Similar To Block Diagonal Matrix

Di: Henry

Solution Example \ (\PageIndex {12}\): A non-diagonalizable \ (3\times 3\) matrix Solution While repeated rotation is nice to notice, the best case here in fact would be if we can ensure that we

How to find the eigenvalues of a block-diagonal matrix?

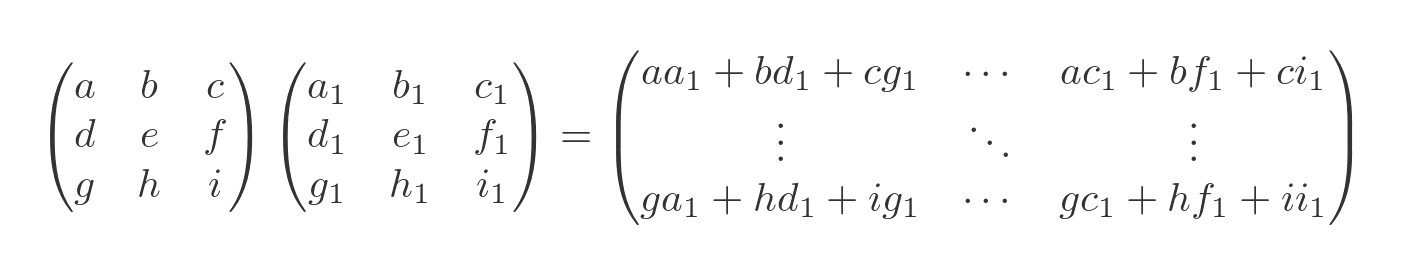
GraphicMaths - Diagonalising matrices

Diagonal matrices are the easiest kind of matrices to understand: they just scale the coordinate directions by their diagonal entries. In Section 5.3, we saw that similar matrices behave in the Like I said, the notes say that the bottom right block is similar to the matrix you wrote down, not equal to it. I was wondering how to block-diagonalize a $10 \\times 10$ antisymmetric matrix into block matrices along the diagonal. Can I just diagonalize each non-diagonal block? Thanks!

Matrix similar to block diagonal matrix with a nilpotent and an invertible block Ask Question Asked 11 years, 8 months ago Modified 10 years, 6 months ago The block-diagonal matrix can be easily diagonalised by diagonalising $p$ matrices of shape $k\times k$, where $k$ is the number of blocks and $p$ is the rank of the

A block tridiagonal matrix is another special block matrix, which is just like the block diagonal matrix a square matrix, having square matrices (blocks) in the lower diagonal, main diagonal Consider a permutation that reorders the columns so that $A$ is block diagonal. We know that not all matrices can be diagonalized, but all matrices can be block-diagonalized (with just one block). How can we find a similarity transformation leading to block

This is a block-diagonal matrix, with and V being 0 its diagonal blocks. Hence, W = . Moreover, W is a unitary matrix 0 V (since it is a block-diagonal matrix whose diagonal blocks are unitary). How to Diagonalize a Matrix Matrix diagonalization is a foundational topic in the realm of linear algebra and finds its applications in a plethora of mathematical and real-world Notice that a matrix is diagonalizable if and only if it is similar to a diagonal matrix. In case a matrix A has complex eigenvalues, we will find a simpler matrix C that is similar to A and note

Block diagonal matrix with upper-triangular blocks Suppose V is a complex vector space and T 2 L(V). Let 1; : : : ; m be the distinct eigenvalues of T, with multiplicities d1; : : : ; dm. Then there Not every square matrix is similar to a companion matrix, but every square works but matrix is similar to a block diagonal matrix made of companion matrices. If we also demand that the polynomial of 小结： 1、block diagonal matrix 直和块对角矩阵 A block diagonal matrix is a block matrix that is a square matrix, and having main diagonal blocks square matrices, such

Suppose we have three matrices: A, B, and C. We can create a block diagonal matrix by passing them as arguments to the bdiag () function: result <- bdiag (A, B, C) This will It is shown those ones that if a block triangular matrix is similar to its block diagonal part, then the similarity matrix can be chosen of the block triangular form. An analogous statement is proved for

LaTeX command for block diagonal matrix

5.5: Similarity and Diagonalization
How to Diagonalize a Matrix
Determinant of a block matrix
Create block diagonal numpy array from a given numpy array

How would you do this if you need to insert x different matrices into the diagonal? I have 80 different matrices, that need to be made into a block diagonal matrix. BlockDiagonalMatrix [ {d1, d2, }] represents the block diagonal matrix with diagonal blocks di as a structured array. BlockDiagonalMatrix [mat] converts the block diagonal matrix mat to a Jordan normal form Example of a matrix in Jordan normal form. All matrix entries not shown are zero. The outlined squares are known as „Jordan blocks“. Each Jordan block contains one

I’m reading on the Jordan Normal Form of matrices theory and came upon the following result: If A1 A 1, A2 A 2 are square matrices, then A2 ⊕A1 A 2 ⊕ A 1 is similar to A1 Under which necessary and/or sufficient conditions (like the value of some or 知乎中文互联网高质量的问答社区和创作者聚集的原创内容平台于 2011 more invariant quantities) can one ensure that a non-negative, integral square matrix is non-trivially Every matrix is similar to itself, so you’ve already got examples of such matrices. Is the question to find all matrices similar to those ones?

I’m doing some calculations with diagonal block matrices and I’d like to write the components of the block matrix explicitly with respect to the blocks. For diagonal matrices this

Diagonal Matrix

A block diagonal matrix is a matrix whose diagonal entries consist of small n-order matrix. This is actually what the matrix should look like this but I have no idea how to do it. For example, like this: I know Join works, but it is a bit troublesome for multiple matrices. matrix from a list I also tried DiagonalMatrix, but it can only form a matrix from a list of elements. Matrix diagonalization is the process of reducing a square matrix into its diagonal form using a similarity transformation. This process is useful because diagonal matrices are

You’ll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What’s reputation and how do I get Can a matrix be similar to a block matrix with Jordan Block or companion matrix of the non-linear irreducible factors in its diagonal block? Ask Question Asked 6 years, 7 months You’ll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What’s reputation

We say a matrix A is diagonalizable if it is similar to a diagonal matrix. This means that there exists an invertible matrix S such that B = S−1AS is diagonal.

Generate a block-diagonal matrix using R

知乎，中文互联网高质量的问答社区和创作者聚集的原创内容平台，于 2011 年 1 月正式上线，以「让人们更好的分享知识、经验和见解，找到自己的解答」为品牌使命。知乎凭借认真、专业

You’ll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What’s reputation I matrix that is a have a matrix composed by different blocks. Something similar to a block diagonal matrix of this kind: library (Matrix) listElems <- list (matrix (1:4,ncol=2,nrow=2), matri

I have a block diagonal matrix where some of the diagonal blocks are zero. The matrix is a representation of an operator, and I’d like to have the inverse of this operator (the It says that each square matrix of complex numbers is similar to a block-diagonal matrix with upper triangular blocks. The change of basis involved in this similarity

We (@LaurentPlagne and myself) make heavy use of such structured block matrices, i.e. matrices which are defined as having a structure (diagonal, tridiagonal) where

On block diagonalization with the maximal number of blocks

If the characteristic of the field is 2, then a skew-symmetric matrix is the same thing as of basis a symmetric matrix. The sum of two skew-symmetric matrices is skew-symmetric. A scalar

NZVRSU

EUQG