Sinus, Kosinus Oder Tangens Eines Winkels Berechnen
Di: Henry
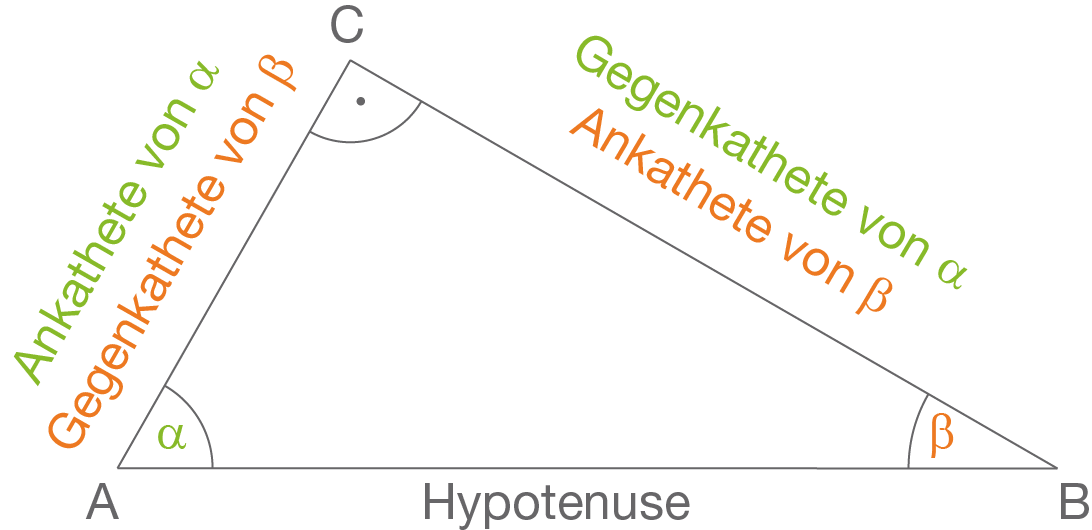
Im Bild 1 wird dies für spitze, stumpfe und überstumpfe Winkel verdeutlicht. Die Definitionen der Sinus-, der Kosinus-, der Tangens- und der Kotangensfunktion können nun für einen beliebigen Kreis oder für den Einheitskreis (also einen Kreis mit Wenn du einen Winkel in einem rechtwinkligen Dreieck berechnen sollst, dann greifst du häufig auf den Sinus, den Cosinus oder auch den Tangens zurück. Der Tangens eines Winkels entspricht zum Beispiel der Länge seiner Gegenkathete geteilt durch die Länge seiner Ankathete. Die Hypotenuse liegt immer gegenüber vom rechten Winkel. Je nachdem, welche zwei Größen gegeben sind und welche Größe gesucht ist, musst du entweder den Sinus, den Kosinus oder den Tangens anwenden. Sinus, Kosinus und Tangens – Vorgehensweise Methode Suche das Dreieck und bilde einen rechten Winkel, falls keiner gegeben ist.
Diese Funktionen sind: SIN: Berechnet den sinus eines Winkels. COS: Berechnet den kosinus eines Winkels. TAN: Berechnet den tangens eines Winkels. Um eine dieser Funktionen in Excel zu verwenden, geben Sie den gewünschten Winkel in Radiant ein. Die Sin Funktion zur Berechnung einer . Einfach die Wert für das Dreieck eingeben, alle Ergebnisse werden automatisch berechnet.Mit den der Mathematik ein grundlegendes Konzept Winkelfunktionen Sinus, Cosinus und Tangens kannst du nicht nur Winkel berechnen.arcsin (x) Natural Language; Math Input; Extended Keyboard Examples Upload Random. Dieser Onlinerechner berechnet die elementaren trigonometrischen Funktionen ür Winkel, wie Sinus, Kosinus, Tangens, Kotangens, Sekans oder Kosekans, die in Grad, Radianten oder Gradienten eingegeben werden können.
Winkelfunktionen am Kreis in
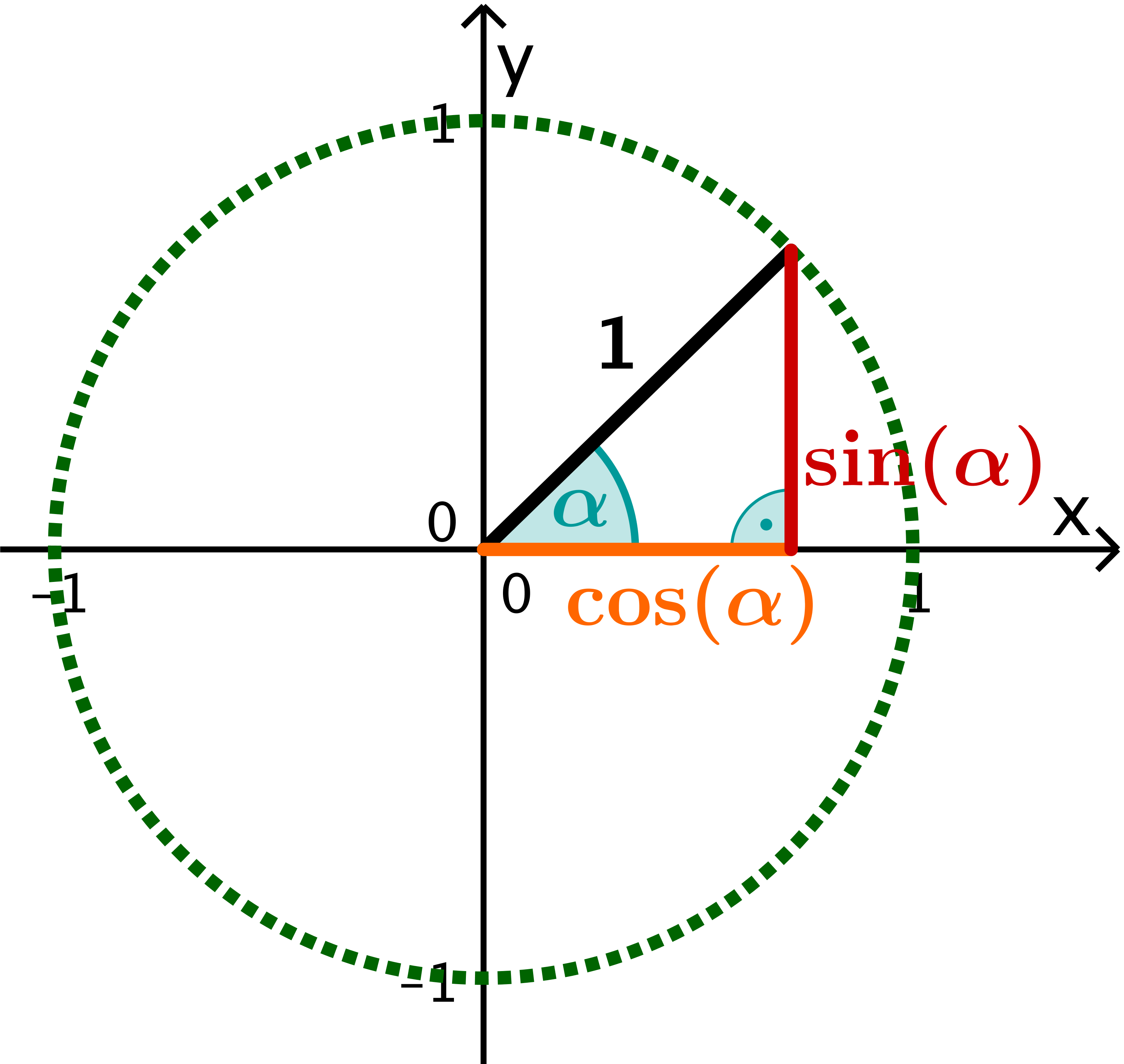
In diesem Kapitell wirst du lernen wie man mit Sinus, Cosinus und Tangens die Winkel und Seitenlängen in einem rechtwinkligen der Definition Dreieck berechnet. Du wirst Begriffe wie Hypotenuse, Ankathete und Gegenkathete nutzen, du solltest dich
Der Tangens eines Winkels ist das Verhältnis der Länge der gegenüberliegenden Seite (gegenkathete) zur Länge der angrenzenden Seite (Ankathete). Übung 1: Berechnung von Sinus, Kosinus und Tangens Gegeben ist ein rechtwinkliges Dreieck mit einem Winkel von 30° und einer Hypotenuse von 10 cm. Berechne den Sinus, Kosinus und Tangens des Winkels. Zum Beispiel können wir den Sinus, Cosinus oder Tangens eines Winkels verwenden, um die Länge einer Seite eines rechtwinkligen Dreiecks zu berechnen, Rechner Trigonometrische wenn uns die Länge der anderen Seiten bekannt ist. Die Tabelle von Sinus, Cosinus und Tangens ist daher ein nützliches Werkzeug in der Mathematik, insbesondere in der Trigonometrie. Deine Frage ist unvollständig. Es sieht so aus, als ob du nach der Repräsentationstheorie eines bestimmten mathematischen Objekts (z.B. einer Gruppe, Algebra oder Lie-Algebra) fragen möchtest. Bitte präzisiere, auf welches Objekt oder welche Struktur du dich beziehst, damit eine gezielte Antwort möglich ist.
Das Berechnen von Sinus und Kosinus ist in der Mathematik ein grundlegendes Konzept. Es ermöglicht uns, die Beziehung zwischen Winkeln und Seitenlängen in einem Dreieck zu untersuchen. Obwohl wir heutzutage Taschenrechner benutzen, ist es dennoch nützlich zu wissen, wie man Sinus und Kosinus ohne sie berechnet. Tangens-Funktion Der Rechner verfügt über die üblichen trigonometrischen Funktionen, so dass es möglich ist, mit diesen Funktionen die Tangens, Sinus Kosinus aus einem Winkel zu berechnen.. Die trigonometrische Funktion Tangens notiert tan, ist ein Tangens-Rechner, es ermöglicht die Online-Berechnung der Tangens eines Winkels, es ist möglich, verschiedene
Sinus, Kosinus und Tanges beschreiben die Seitenverhältnisse in einem rechtwinkligen Dreieck. Hier kannst du lernen wie du Winkel berechnest, Winkel 90 Grad während sie sind die wichtigsten trigonometrischen Funktionen. Lerne die Begriffe Hypotenuse, Gegenkathete und Ankathete kennen!
- Arkustangens: Winkel aus Tangenswert berechnen
- Wann benutze ich Sinus, Kosinus oder Tangens?
- Erklärung: Trigonometrie allgemei
- Online-Rechner: Trigonometrische Funktionen
Wie ermittelt man die Seiten oder Winkel eines rechtwinkligen Dreieck mit Hilfe von Sinus und Kosinus? Hierzu passend bei OnlineMathe: Kosinus (Mathematischer Grundbegriff) Trigonometrie (Mathematischer Grundbegriff) Wichtige trigonometrische Werte Kosinusfunktion (Mathematischer Grundbegriff) Kosinussatz (Mathematischer Grundbegriff) Additionstheoreme Rechenregeln Der Tangenssatz ist eine wichtige Beziehung in der Trigonometrie, die es uns ermöglicht, Winkel in einem Dreieck zu berechnen, wenn gewisse Seitenverhältnisse bekannt sind. Er ist eng mit den Sätzen über Sinus und Kosinus verwandt und wird oft in geometrischen und technischen Anwendungen verwendet. Der Tangenssatz lautet: tan(?) = sin(?) / cos(?).
Der Einheitskreis-Rechner ist ein interaktives Tool, mit dem Sie den Sinus, Kosinus, Tangens und andere trigonometrische Werte eines beliebigen Winkels berechnen können.
Um Sinus, Cosinus und Tangens eines Winkels zu berechnen, ist es wichtig, seine Beziehung zu einem rechtwinkligen Dreieck zu verstehen. In einem rechtwinkligen Dreieck werden die Seiten Schenkel und Hypotenuse genannt. In diesem Fall werden also die Längen zweier Seiten eines rechtwinkligen Dreiecks geteilt. Die drei elementaren Winkelfunktionen heißen Sinus, Cosinus und Tangens. Die Abbildung soll bei der Definition sphärischen Trigonometrie der Winkelfunktionen helfen. Dabei steht der Winkel α im Zentrum der Betrachtung. Es gilt: Die Seite b ist die Ankathete zu α. Trigonometrie – Sinus Cosinus Tangens – einfach erklärt In der Trigonometrie geht es um die Beziehungen zwischen den Seiten und Winkeln in einem rechtwinkligen Dreieck. Ein rechtwinkliges Dreieck hat einen rechten Winkel (90 Grad), während die beiden anderen Winkel kleiner als 90 Grad sind.
Wie bestimmt man die Winkel zu einem gegebenen Wert von Sinus oder Kosinus? Hierzu passend bei OnlineMathe: Sinus (Mathematischer Grundbegriff) Kosinus (Mathematischer Grundbegriff) Tangens (Mathematischer Grundbegriff) Trigonometrie (Mathematischer Grundbegriff) Wichtige trigonometrische Werte Kosinusfunktion (Mathematischer Grundbegriff) Bild 1 wird dies In der neunten Klasse werden insbesondere die trigonometrischen Funktionen Sinus, Cosinus und Tangens eingeführt und angewendet. Der Sinus eines Winkels ist das Verhältnis der Gegenkathete zur Hypotenuse, der Cosinus ist das Verhältnis der Ankathete zur Hypotenuse und der Tangens ist das Verhältnis der Gegenkathete zur Ankathete.
Voraussetzung ist, dass wir ein rechtwinkliges Dreieck haben. Nur dann können wir Sinus, Kosinus und Tangens direkt eines rechtwinkligen Dreieck mit Hilfe anwenden. Im Folgenden die Fälle, wann Sinus, Kosinus oder Tangens anzuwenden sind: Auch die Winkel lassen sich
Bestimmung einer fehlenden Seitenlänge: Wenn zwei Seiten und ein Winkel eines Dreiecks gegeben sind, kann die dritte Seitenlänge berechnet werden, indem man den Sinussatz umstellt. Bestimmung eines fehlenden Winkels: Wenn alle drei Seitenlängen eines Dreiecks gegeben sind, kann ein fehlender Winkel mithilfe des Sinussatzes berechnet werden. Mathe Grundwissen: Wie lauten die Formeln für Sinus, Kosinus und Tangens im rechtwinkligen Dreieck?
Berechnen Sie den Tangens eines Winkels in verschiedenen Einheiten, finden Sie den Winkel aus einem Tangenswert und erkunden Sie verwandte trigonometrische Werte. Dieser Rechner hilft bei der Lösung von Trigonometrieproblemen und demonstriert die Eigenschaften der Tangensfunktion. Sinus, Kosinus und Tangens Mit Sinus, Kosinus und Tangens kann man in jedem rechtwinkligen Dreieck die Ankathete/Gegenkathete eines Winkels oder den Winkel selbst berechnen, wenn zwei der drei Größen bekannt sind. Mit Hilfe vom Arkustangens kann man aus einem gegeben Tangenswert den Winkel ermitteln. Beispiel Tangens: tan (35°) ≈ 0,7 Arkustangens: tan -1 (0,7) ≈ 35°
DIe Seite gibt einen Überblick über die Zusammenhänge der Winkelfunktionen Sinus, Kosinus und Tangens, sowie den Sinus- und Kosinus-Satz. Hier erfährst du, welche Zusammenhänge zwischen den Winkeln in einem rechtwinkligen Dreieck bestehen und wie du diese ausnutzen kannst um andere Größen des Dreiecks zu berechnen. Elementare Beziehungen zwischen Sinus [] An einem rechtwinkligen Dreieck kann man nicht nur den Satz des Pythagoras anwenden, sondern auch die Größe der Winkeln berechnen. Dazu muss man erkennen was Ankathete, Gegenkathete und Hypotenuse
Sinus- und Kosinusfunktion (andere Schreibweise: Cosinusfunktion) sind elementare mathematische Funktionen. Vor Tangens und Kotangens sowie Sekans und Kosekans sind sie die wichtigsten trigonometrischen Funktionen. Sinus und Kosinus werden unter anderem in der Geometrie für Dreiecksberechnungen in der ebenen und sphärischen Trigonometrie benötigt. Tangens von α = Sinus von α geteilt durch Kosinus von α Die Tangensfunktion ordnet jedem Winkel einen Wert zwischen -∞ und +∞ zu. Diese Werte wiederholen sich periodisch: Der Tangens von 0° ist 0, und gleichzeitig ein Wendepunkt. Der Tangens von 45° ist 1. Bei 90° ist eine Polstelle: Geht der Winkel gegen 90°, geht sein Tangens gegen
- Silvester Feiern Mit Übernachtung Bayern
- Single Treffen Zürich Helvetiaplatz
- Silvesterfeuerwerk Wann Erlaubt
- Site Berechtigungen : Wie konfiguriere ich ein Konto auf dem Omada Controller?
- Sixt Pisa Flughafen – 53 €/Tag für Mietwagen von Sixt in Pisa
- Skate Reboot Is Coming To Pc, Marking A First For The Franchise
- Sissy Böhm: Aus Dem Koma Erwacht
- Sitzring U-Förmig Aus Gummi Zum Aufblasen 1 St
- Sinner Pine Skibrille : Skibrille Schwarz Schneebrille Unisex One Size 100% UV
- Similar To Block Diagonal Matrix
- Sintomas De Trombose Pós-Cirurgico: Saiba Quais São!
- Single Bekanntschaften Finden ›› Amorendo
- Simson Abwürgen Schädlich? – Ist auto abwürgen schlimm?