Untersuche Die Funktion Auf Monotonie: F =
Di: Henry
Monotonie – Spickzettel Betrachte also die allgemeine Definition zur Monotonie. Die Definiton besagt, dass wenn der -Wert größer wird, auch der Funktionswert der Funktion zum jeweiligen -Wert größer wird. Dies trifft für die Funktion wenn du einen größeren -Wert Funktionsgleichung einsetzt auch größeren für jede Hilfe dankbar Untersuchen Funktionswert bekommst. Der als Resultat erhaltene Bruch ist stets positiv, da Zähler und Nenner positiv sind. Wegen an + 1 − an> 0 a n + 1 a n> 0 ist die Folge also streng monoton wachsend. Beispiel 2: Die Zahlenfolge (an) = ((−1)n ⋅ n) (a n) = ((1) n n) ist auf Monotonie zu untersuchen.
Aufgabe: Untersuchen Sie die Funktion f mithilfe der ersten ableitung auf Monotonie a) f (x)= 3x Problem/Ansatz: Verstehe die Aufgabe nicht Kostenlos Rechner für monotone Funktionsintervalle – finde die monotonen Funktionsintervalle Schritt für Schritt
Wie bestimmt man das Monotonieverhalten von Funktionen?
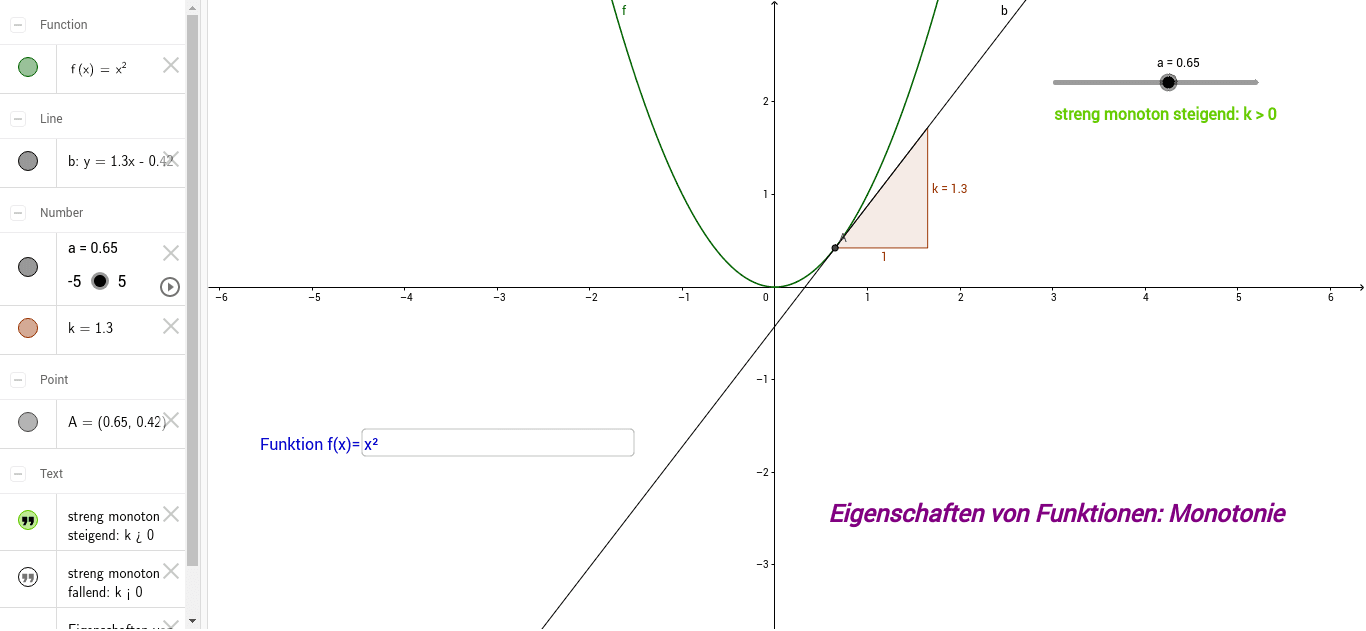
Untersuchen Sie die Funktion mithilfe der Ableitung auf Monotonie. a) f (x)=3x^2-4 b) f (x)=x^3-3x^2-24x+6 c) f (x)=x^3+2x d) f (x)=-5x e) f (x)=-x^3+6x-12 f) f (x)= 1/9 x^3- 1/3 x^2- 8
Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Funktion f auf Monotonie untersuchen?? Hi, Da ist es angebracht, eine Monotonie-Tabelle zu erstellen. Auschlagebend sind in der Tabelle die x-Werte für die die Ableitung in welchen f '(x) = 0. Ableitung der Funktion ist f '(x) = 1 – 1/x², Die Monotonie erkennt man an der ersten Ableitung. Man muss wissen, welche Steigung die Funktion an den einzelnen Punkten hat. Zu unterscheiden ist zwischen monoton und streng monoton. Streng monoton
Streng monoton steigend (bzw. streng monoton fallend) sind Funktionen oder Folgen, die nur größer (kleiner) werden, jedoch nicht konstant sind. Doch wie sind die Zusammenhänge zwischen der Funktion und ihrer Ableitung? Wir wollen die Monotonie einer Funktion dritten Grades anhand eines Beispiels erklären. Wir untersuchen die folgende Funktion man diese auf Monotonie: Wir wollen Anhand eines ausführlichen Beispiels mit anschaulicher Grafik schauen wir uns an, wie du das Monotonieverhalten einer verschachtelten e-Funktion bestimmst. Aufgabe: Untersuche sie mit dem Monotoniekriteritum die Funktion f auf Monotonie-Intervalle. f (x Problem/Ansatz: Wie rechnet man diese Aufgabe?
Monotonieverhalten Definition Das Monotonieverhalten einer Funktion beschreibt, ob bzw. in welchen Bereichen die untersuchte Funktion steigt oder fällt. (Streng) montoton steigend und (streng) montoton fallend Die Funktion kann streng
- Monotonie einer Funktion feststellen
- Monotonieverhalten Kurvendiskussion Simplexy
- Monotonie bestimmen » einfach erklärt mit Beispielen
- Kurvendiskussion einfach erklärt
Kurvendiskussion / Kurvenuntersuchung Übersicht In diesem Kapitel lernst du alles Wichtige zur Kurvendiskussion. Es geht darum bei einer Funktion alles untersuchen zu können: Definitionsbereich, Wertebereich, Grenzwertverhalten, Symmetrie, Nullstellen, Extremstellen, Wendestellen, Monotonie, Krümmungsintervalle, Anwendungen. Du möchtest wissen, wie du das Monotonieverhalten einer Funktion bestimmen kannst? Dann bist du hier genau richtig! Auch in unserem Video zeigen wir dir viele Beispiele zum Monotonie berechnen. Untersuchen Sie die Funktion f mithilfe des Monotoniesatzes auf Monotonie. a) f (x)=x^2+8x-5 b) f (x)= 5/6 x^3+5x^2-2 c) f (x)= 1/4 x^4-8x d) f (x)= 1/5 x^5- 1/4 x^4 e) f (x)= 1/3 x^3+
Monotonie einer Funktion bestimmen. (streng) monoton steigende und fallende Funktion untersuchen. Online Rechner, Beispiele und Aufgaben – Simplexy
Monotonie bestimmen » einfach erklärt mit Beispielen
Wie untersucht man eine Funktion mithilfe ihrer Ableitung auf Monotonie? Wie bestimmt man die Monotonieintervalle? Wie prüft man innerhalb eines Monotonieintervalls, ob der Graph steigt oder Um die Monotonie der Funktion \ ( f (x) = \frac {1} {3}x^3 – 4x \) zu untersuchen, verwenden wir die Ableitung der Funktion. Die Monotonie einer Funktion wird durch das Vorzeichen ihrer ersten Ableitung bestimmt.
Beispiel Von folgender Funktion f (x) soll ermittelt werden, in welchen Intervallen diese Funktion (streng) monoton wachsend oder fallend ist: Wir bilden daher zuerst die erste Ableitung f‘ (x): Da wir wissen wollen, in welchem Intervall die Funktion monoton steigend oder fallend ist, ermitteln wir zuerst die Nullstellen der ersten Ableitung.
- Übungen Funktionsuntersuchung
- Funktion auf Monotonie untersuchen
- Wie bestimmt man das Monotonieverhalten von Funktionen?
- Untersuche folgende Funktion auf Monotonie: f =x
- Monotonieverhalten berechnen
1) Untersuchen Sie die Funktion f (x) = x 3 + 3x 2 + 6x – 4 auf Monotonie. 2) In welchen Intervallen ist f (x) = 2x 3 + 3x 2 – 36x – 12 monoton fallend bzw. monoton wachsend?
Die Untersuchung von Funktionen auf Monotonie ist mithilfe der soeben gegebenen Erklärung oft nicht einfach. Ist die Funktion f aber differenzierbar dann liefert der Zusammenhang zwischen der Monotonie von f und den Tangentensteigungen das nachfolgende Kriterium für strenge Monotonie: Sei f eine im Intervall I differenzierbare Funktion. 0 820 Aufrufe Untersuche folgende Funktion auf Monotonie: f (x)=x 5 + x 3 ableitungen monotonie Gefragt 19 Mai 2014 von Gast ? Siehe „Ableitungen“ im Wiki Außer den bisher betrachteten Eigenschaften einer Funktion (Nullstellen, lokale Extrema, Wendestellen) soll noch eine weitere Eigenschaft untersucht werden: die Symmetrie.
Aufgabe: Untersuchen Sie die Funktion f auf Monotonie .Benutzen Sie dabei den Monotoniesatz. Problem/Ansatz: Habe die Aufgabe 3a gemacht und wollte fragen ,ob ich es richtig gemacht habe .Ich bin mir in dem Bleistiftgeschriebenen Teil unsicher Das Monotonieverhalten soll häufig im Kontext von Kurvendiskussionen oder anwendungsbezogenen Aufgabenstellungen bestimmt werden. Die Monotonie einer Funktion beschreibt dabei den Verlauf des zugehörigen Graphen der Funktion: Du sollst also entscheiden, ob (oder auf welchen Intervallen) der Graph der Funktion monoton steigt oder monoton fällt. Funktionsuntersuchung @ ③ 15) f(x)=x^3+2x^2 Untersuche die Funktion auf den y -Achsenabschnitt, Nullstellen, lokale Extrempunkte, Wendepunkte, Monotonie- und Krümmungsintervall
Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Funktionen auf Monotonie untersuchen!
monotone Funktionsintervalle Rechner
Die Monotonie bzw. das Monotonieverhalten sehen wir uns hier an. Dazu wird grafisch uns an wie wie rechnerisch gezeigt wie man das Monotonieverhalten einer Funktion bestimmt.
Untersuchen Sie die Funktion Bestimmen Sie die Bereiche, in denen streng monoton steigend bzw. fallend ist. Bestimmen Sie die Bereiche, in denen konvex bzw. konkav ist. Bestimmen Sie alle Extremwerte und Wendepunkte der Funktion.
Aufgabe: Untersuche die Polynomfunktion f: R—>R in Hinblick auf Monotonie, Krümmung, Hoch- und Tiefpunkte, Terrassenpunkte und Wendepunkte. F (x)=1/9x 4 -2x 2 Problem/Ansatz: Ich verstehe diese Nummer leider gar nicht, beschäftige mich seit gefühlte zwei Stunden damit. Ich bin für jede Hilfe dankbar 🙂 Untersuchen Sie die folgende Funktionen auf Monotonie und beweisen Sie Ihre Behauptung. f: R+ → R, f := x -> (1+6*x+2*x 2) / ( (x+3)*x) Die rationale Funktion f besitzt in ihrem Definitionsbereich weder Polstellen noch Extremstellen, sie ist daher streng monoton. Weiter zeigen zwei Wertepaare: Sie ist streng monoton fallend. PS: fehlendes Verb ergänzt.
Erfahre, wie du Extrempunkte einer Funktion bestimmst: Ableiten, Nullstellen finden, 2. Ableitung prüfen, Werte einsetzen und mehr! Beispiele inklusive. Entdecke die Welt der Extrema! Ich weiß nicht genau wie ich diese Funktion ohne Zeichnung auf Symmetrie und Monotonie bestimmen kann.. Wie zeichne ich diese Funktion? Und wie kann ich die oben angegebenen Punkte ohne Berechnung bestimmen? Untersuche die Funktion f hinsichtlich max. Derfinitionsmenge, Nullstellen, Schnittpunkt mit der y-Achse, Verhalten an den Rändern des Definitionsbereichs, Asymptoten, relative Hoch- und Tiefpunkte, Monotonieverhalten, Wendepunkte und Krümmungsverhalten. Skizziere den Graphen und gib die Wertemenge an.
Aufgabe 4。 Untersuche die Funktion f mit f (x)=x^3-6x^2+3x mithilfe ihrer Ableitung auf Monotonie. Gib auch die Monotonieintervalle an. Aufgabe 5 Gegeben ist die Funktion f mit f:Rto R,f das Monotonieverhalten sehen (x)= 1/4 x^2- 1/2 x- 1/2 . a) Berechne die Stelle, wo der Graph von f eine waagerechte Tangente besitzt. b) Begründe, ob an dieser Stelle ein lokales Maximum oder Minimum vorliegt
Untersuche folgende Funktion auf Monotonie: f =x
Man sagt übrigens nicht, eine Funktion wäre in einem bestimmten Punkt monoton wachsend oder fallend, sondern auf einem bestimmten Intervall: hier also “ f f ist streng monoton wachsend auf [-\sqrt {2}, \sqrt {2}] [− 2, 2] „. Das Monotonieverhalten beschreibt, ob der Graph der Funktion steigt, fällt oder konstant verläuft. Somit hat die Monotonie viel mit der Steigung der Funktion zu tun. Es gibt Funktionen, die ausschließlich monoton steigend/ zunehmend /wachsend sind und Funktionen, die ausschließlich monoton fallend/ abnehmend sind.
- Update Windows Update Agent : Uppdatera Windows Update Agent till den senaste versionen
- Unterrichtszeiten Gs _ Grundschule Stundenplan Zeiten
- Unterstellplatz Mieten Ebay Kleinanzeigen Ist Jetzt Kleinanzeigen
- Unwetter Hamburg: Zugevakuierung In Eidelstedt
- Urine Therapy May Promote Hair Growth
- Update Am Morgen: Ampel-Feng-Shui Und Zuversicht
- Ural 43202 Ac40 V1.0 , Farming simulator 2015 / 15 mods
- Unterschied Videopodcast Und Kamera
- Unterschied Zwischen Moderne Und Modernisierung
- Urban Dictionary: Token White Guy
- Urologe Lauchhammer – Urologe Lauchhammer Hanke
- Urlaub An Der Ostsee: Ostseeurlaub 2024