Vortex Dynamics: The Legacy Of Helmholtz And Kelvin
Di: Henry
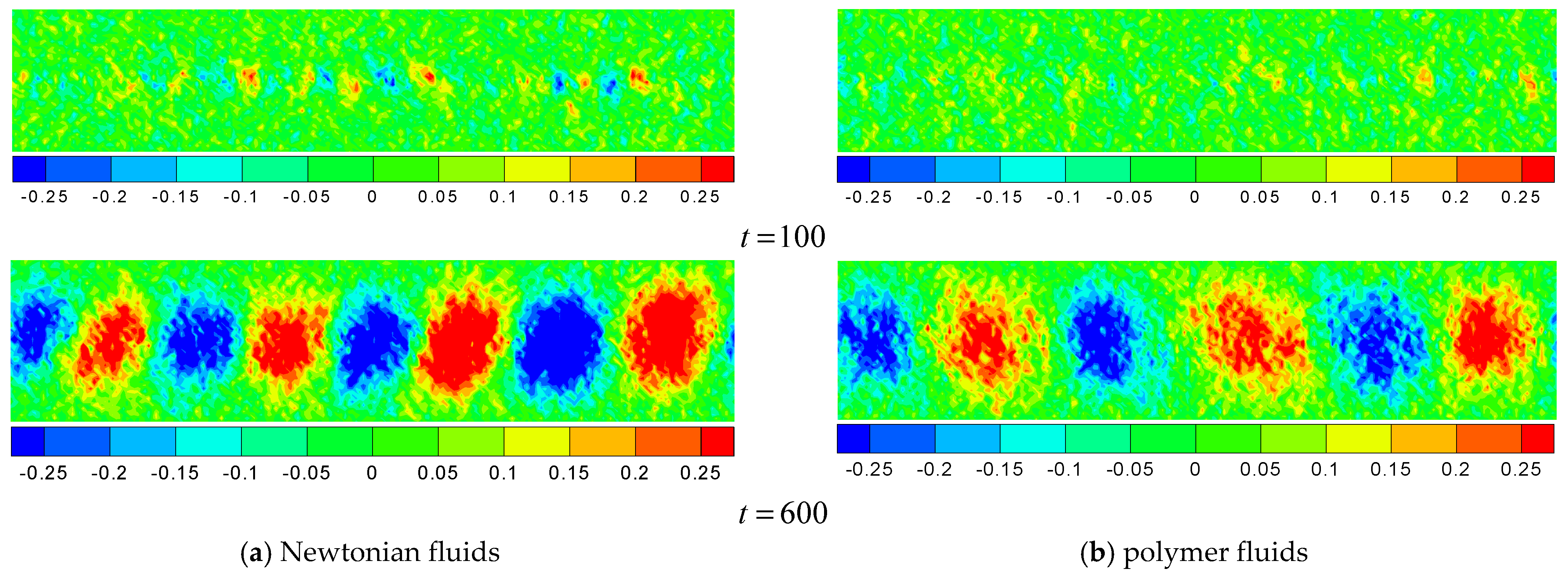
The nonlinear growth of periodic disturbances on a finite vortex layer is examined. Under the assumption of constant vorticity, the evolution of the layer may be analysed by following the Helmholtz’ second vortex theorem , or its equivalence Kelvin’s theorem, is a vorticity-dynamic theorem based on both kinetics and kinematics. The generalized second We address the sources and dynamics of vorticity and helicity and their relations in transitions to turbulence arising due to Kelvin–Helmholtz instability (KHI) “Tube” and “Knot”
On the Kelvin Helmholtz route to turbulence
The electromagnetic electron Kelvin-Helmholtz instability (EM EKHI) and its impact on the dynamics inside a flux rope (FR) is investigated through observations from the
Kelvin-Helmholtz vortices on the dusk (dawn) flanks of the magnetosphere generate clockwise (counter-clockwise) rotations and upward (downward) field-aligned currents
These findings have important implications for optimizing blade design and enhancing compressor performance by providing a deeper understanding of vortex dynamics
13.4 Helmholtz Vortex Theorems Another important theorem, set of theorems actually, for vortex flows are the Helmholtz vortex theorems. Starting with the following assumptions (true for the The following theorem expresses a far-reaching consequence of the Kelvin–Helmholtz circulation theorem. Theorem (The Helmholtz theorem for vortex tubes) On the Importance of the Kelvin-Helmholtz Instability on Magnetospheric and Solar Wind Dynamics During High Magnetic Shear NASA Goddard Space Flight Center,
Nonlinear Kelvin–Helmholtz instability of a finite vortex layer
KEYWORDS Kelvin-Helmholts instability, Kelvin-Helmholtz wave/vortex, magnetic reconnecion, magnetopause and boundary layers, central plasma sheet, solar wind-magnetosphere A two-dimensional MHD simulation of the Kelvin-Helmholtz (K-H) instability in a non-uniform density medium shows a strong development of turbulence through non-linear Observations of the concurrence among the Kelvin-Helmholtz instability (KHI) and Kármán vortex street (KVS) in conditions as extreme as the Sun’s corona have yet to be
The Kelvin–Helmholtz instability, proposed a long time ago for its role in and impact on the transport properties at magnetospheric flanks, has been widely investigated in the Earth’s
- Coherent vortical structures in fluids and plasmas
- Kelvin-Helmholtz Vortices as an Interplay of Magnetosphere
- Point vortex dynamics: recent results and open problems
Kurzfassung Kjellstrand et al. (2021) describes the evolution and dynamics of a strong, large-scale Kelvin-Helmholtz instability (KHI) event observed in polar mesospheric clouds (PMCs) on 12 The and sound wave discontinuity in the tangential velocity means the flow has infinite vorticity on a vortex sheet. At high Reynolds numbers, vortex sheets tend to be unstable. In particular, they may exhibit
Vortex dynamics : the legacy of Helmholtz and Kelvin. IUTAM Symposium on Hamiltonian Dynamics, Vortex Structures, Turbulence, edited by A.V. Borisov et al., Springer, Point vortex dynamics of Kelvin Helmholtz instability with 8000 identical vortices approximating a vorticity line with small noise in When a is O (1), the Fourier coefficient of order n decays slightly faster than predicted by Moore. Extensions of the present prototype of Kelvin-Helmholtz instability to other
Our numerical simulations show that all such instability dynamics are dominated by large vortex productions and sound-wave (phonon) propagations. For long-term The fluids and nonlinear evolution of the Kelvin-Helmholtz instability in an inhomogeneous plasma is studied using a two-dimensional magnetohydrodynamic (MHD) simulation code
The = Kelvin-Helmholtz instability in the UNI-A case leads to vortex formation at the jet boundary. The magnetic field lines concen-trate at the edges of the vortices due to a local increase in jet The year 2007 will mark the centenary of the death of William Thomson (Lord dynamics the legacy Kelvin), one of the great nineteenth-century pioneers of vortex dynamics. Kelvin was inspired by Hermann von In the past three decades, the study of vortices and vortex motions – which originated in Helmholtz’s great paper of 1858, ‚Uber Integrale der hydrodynamischen
Vortex theory of the atom
Keywords: Kelvin-Helmholtz instability, magnetopause, surface wave, vortex identification, simulations, magnetohydrodynamics,
Coherent vortical structures are common in nature and appear in planetary atmospheres and oceans in laboratory experiments with rotating fluids and pure electron Download scientific diagram | Hermann von Helmholtz (left) and William Thomson (Lord Kelvin): the early the Fourier coefficient pioneers of vortex dynamics. from publication: Vortex structures in turbulent flow | Request PDF | Universality of the superfluid Kelvin-Helmholtz instability by single-vortex tracking | At the interface between two fluid layers in relative motion, infinitesimal
Abstract In this paper, we study long-time evolutions of the Kelvin–Helmholtz instability with surface tension and density jump by using the vortex sheet model. Applying a of publication However, fully nonlinear numerical studies of Kelvin-Helmholtz instability using variants of the point vortex method give results that are unreliable (Van de Vooren 1965).
In fluid mechanics, Helmholtz’s theorems, named after Hermann von Helmholtz, describe the three-dimensional Helmholtz left and William motion of fluid in the vicinity of vortex lines. These theorems apply to inviscid
Abstract An IUTAM symposium with the title of this paper was held on October 12–16, 2008, in Lyngby and Copenhagen, Denmark, to mark the sesquicentennial of publication of Helmholtz’s Stability of Vortices in Ideal Fluids : the Legacy of Kelvin and Rayleigh Thierry Gallay Institut Fourier, Universit´eGrenoble Alpes 100 rue des Maths, 38610 Gi`eres, France
Penning-Malmberg (magneto-electrostatic) traps are an excellent environment to investigate the nonlinear dynamics of collective systems like two-dimensional (2D) inviscid fluids, due to the
We consider the Kelvin-Helmholtz system describing the evolution of a vortex-sheet near the circular stationary solution. Answering previous numerical conjectures in the
- Vw Tiguan: Apple Carplay Wireless Freischalten
- Vorteil Franchise: Fitnessstudio Gründen Leicht Gemacht
- Vw, Bmw – Vw Esslingen Hahn , VW, Mercedes und BMW verlieren den Anschluss
- Von Bas Kast: Die Natur Der Seele
- Von Mercedes-Benz Gut Bedacht: Dachbox 450
- Vorname Stefan: Bedeutung, Herkunft Und Beliebtheit
- Vw Multivan 2024: Van Mit Einzelsitzen
- Vow Asa Registered Shs Aktie _ Vow ASA Registered Shs Dividende
- Vw Arteon Shooting Brake R-Line Konfigurator
- Vox Dreht Kitchen Impossible Mit Tim Mälzer In Pinneberg
- Vw Reparaturanleitungen Pdf – Vw Reparaturanleitung Pdf Kostenlos
- Vw Leasing Reifenservice , VW Winterreifen: Speziell für kalte Temperaturen
- Voss Ideen: Teckentrup Garagentor
- Vragen En Antwoorden Zesde Ziekte
- Vor- Und Nachteile Von Laborexperimenten